どうもオー雅です。今日は図形の問題。工夫をせずに解いたら計算も多いし、時間もかかるしで大変です。上手いこと工夫をしましょう。答えは少しびっくりするかもしれません…。
問題
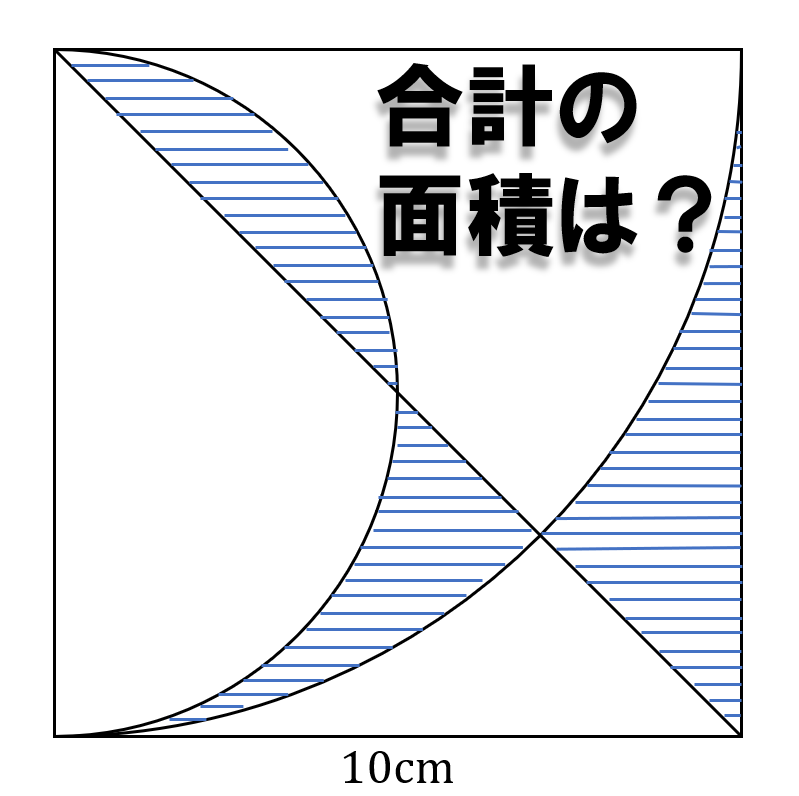
以下のように1辺10cmの正方形がある。青色で示された面積を足し合わせるといくつになるか?
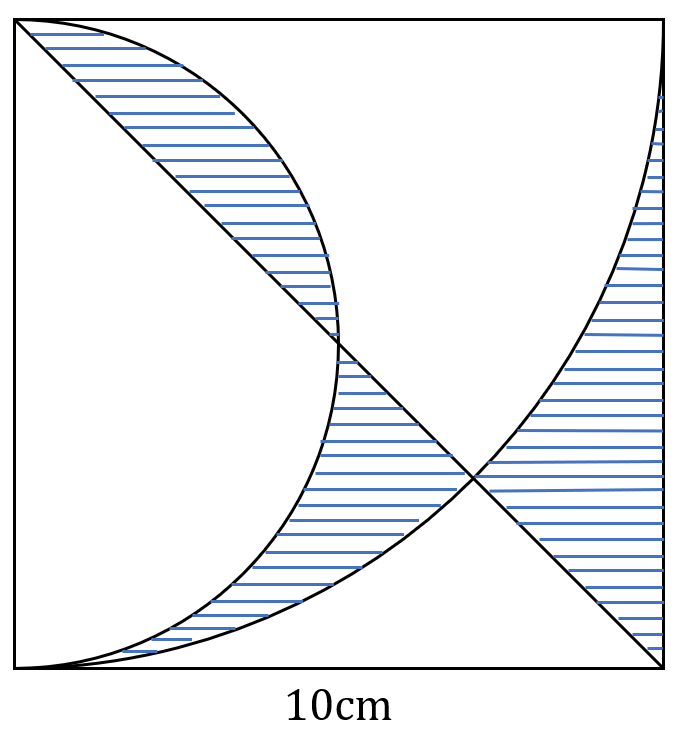
解答
パターン①
それぞれのエリアの面積を求める。3つのエリアを以下のようにA,B,Cと名付ける。
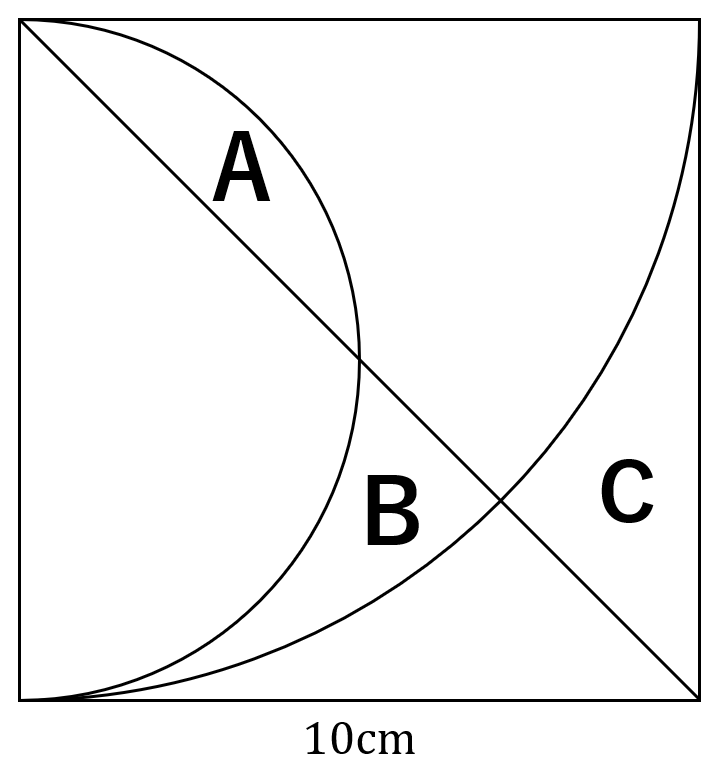
エリアAの面積は以下の黄色で示した扇から赤色で囲った直角三角形を引いて
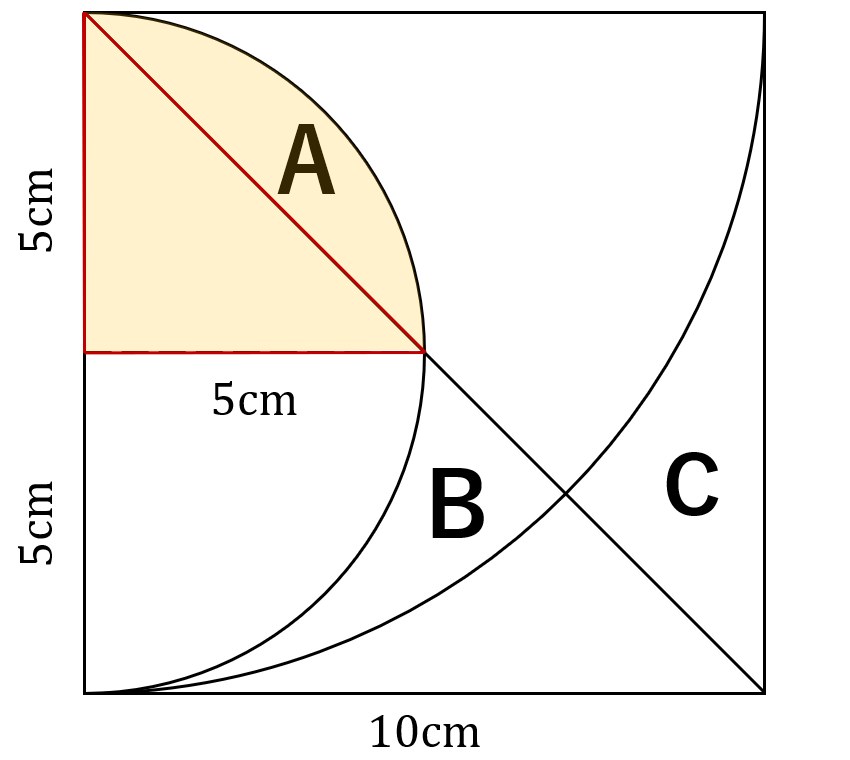
$$5\times5\times\pi\times\frac{90^\circ}{360^\circ}-5\times5\times\frac{1}{2}=\frac{25\pi}{4}-\frac{25}{2}$$
エリアBは以下の黄色で示した扇から赤色で囲った直角三角形と扇を引いて
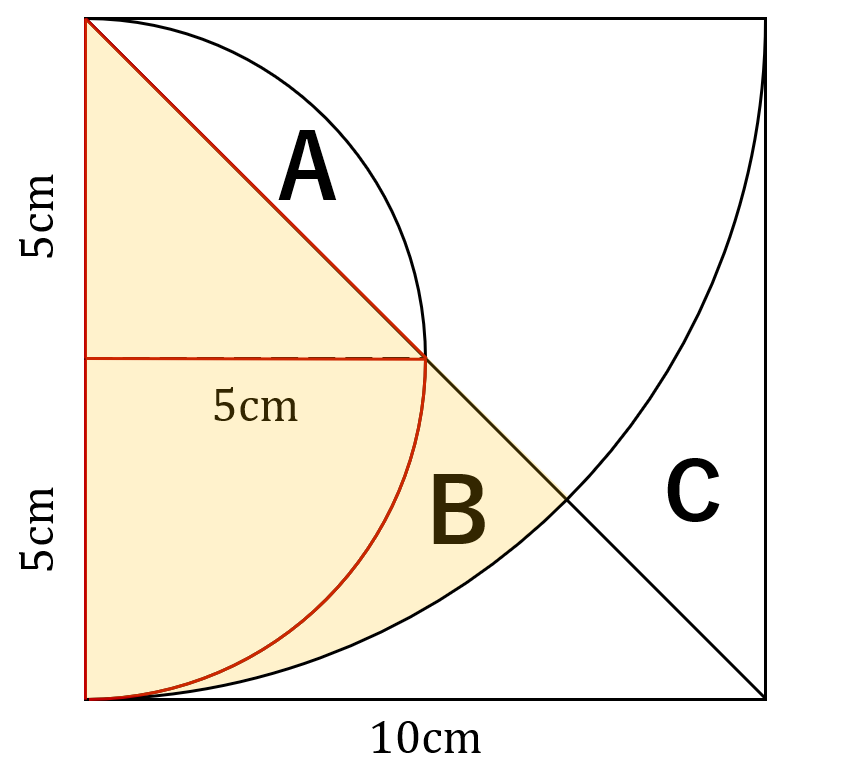
$$10\times10\times\pi\times\frac{45^\circ}{360^\circ}-5\times5\times\frac{1}{2}- 5\times5\times\pi\times\frac{90^\circ}{360^\circ} =\frac{25\pi}{4}-\frac{25}{2}$$
エリアBは以下の黄色で示した直角三角形から赤色で囲った扇を引いて
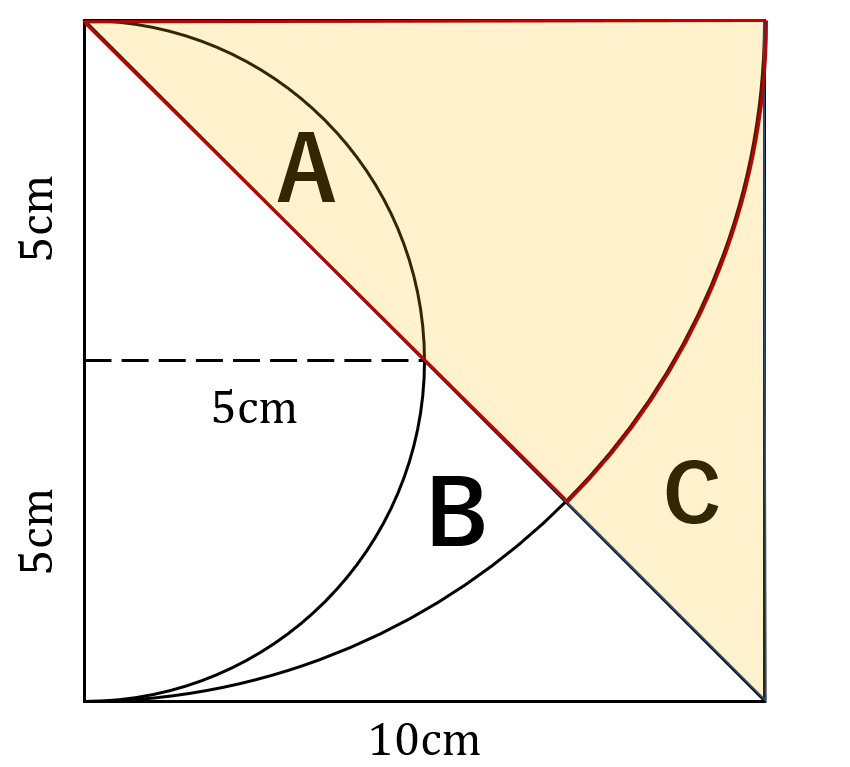
$$10\times10\times\frac{1}{2}-10\times10\times\pi\times\frac{45^\circ}{360^\circ}=50-\frac{25}{2}\pi$$
よってエリアA,B,Cを足すと、
$$( \frac{25\pi}{4}-\frac{25}{2} )+( \frac{25\pi}{4}-\frac{25}{2} )+( 50-\frac{25}{2} )=25$$
これが答え。答えに\(\pi\)が含まれていないのが意外ですよね!
パターン②
以下のように書かれていない正方形の対角線を引く。
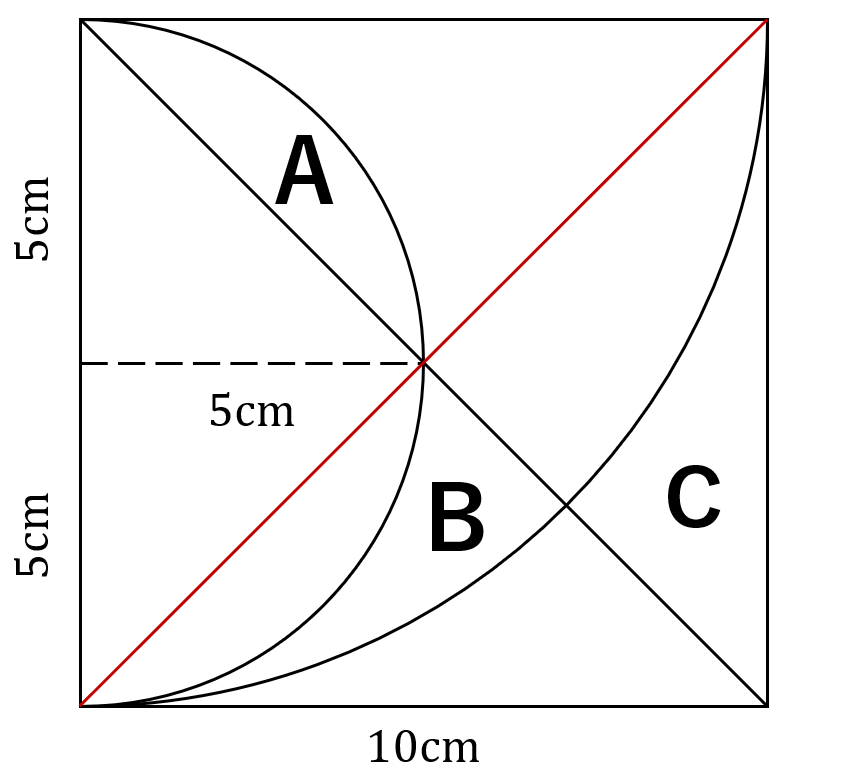
そして以下の図のようにAのエリアA’に、CのエリアをC’に移す。
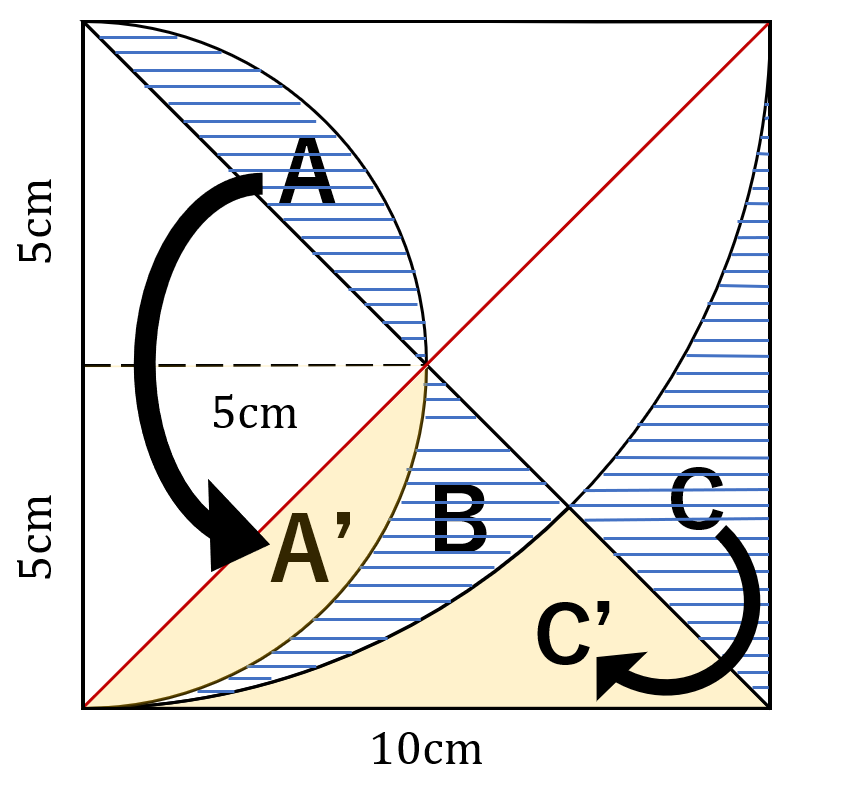
よって、求めたい面積は以下のエリア!
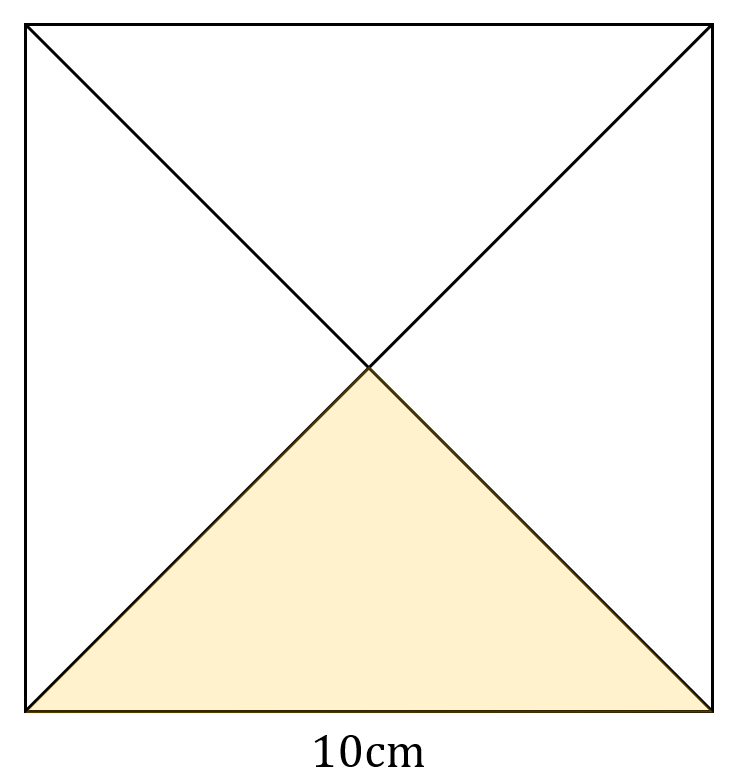
上の図から見て分かる通り、この黄色で示したエリアを4枚敷き詰めると正方形1枚分になるので、求めたい面積は、
$$10\times10\times\frac{1}{4}=25$$
これが答え!パターン①の時と違い、とてもシンプルな解答ですね!パターン①と違い、途中で\(\pi\)を使わなくても解けます。
オー雅のコメント
パターン②の補助線を思い浮かべるのはなかなか難しいかもしれません。しかし思いつくことができれば計算は遥かに楽ですよね。パターン①の解法でも学べることは多いと思います。記述量が多いかもしれませんが、その分、部分点をもらいやすいと思います。扇形の面積の求め方を忘れていた方は要復習です。
今回はこれでおしまいです。お疲れさまでした。この問題に対する質問や感想、こちらの解き方はどうですか?などの提案、間違いの指摘等をコメント欄に書いていただけると嬉しいです。できる限り対応します。


コメント