どうもオー雅です。本日はコメントにてリクエストをいただいた式の値編!
私の初投稿した計算編に通ずる内容が多いため、まずは計算編を見直していただいてからこの式の値編を見ていただくことをお勧めします。
以下の目次の説明を行っていきます。では始めていきましょう。
レベル1:\( \quad 5x-3x \quad(x=3)の値\)
え、余裕じゃん!5×3-3×3で6でしょ!と思った方。間違ってはないですが遠回りしてしまっています。まずは計算を進めてから代入しましょう。
$$5x-3x=2x$$
この \(2x\) に代入した方が遥かに楽でしょう。2×3=6で済みますからね。複雑な問題になればなるほど計算を進めてから代入しないと痛い目にあいます。今のうちに癖をつけておきましょう。
レベル2:\( \quad 2x^2 \quad(x=-3)の値\)
これ答えプラスになるんだっけ?マイナスになるんだっけ?と混乱する方が大多数ですが既に計算編を見ていただいた方ならもう大丈夫ですよね!分からなくなったらばらすのみ!
$$2x^2=2 \times x \times x $$
ここに\(x=-3\)を代入しましょう。
$$2x^2=2 \times x \times x =2 \times (-3) \times (-3)=18$$
これが答えです。カッコつきで代入することを忘れずに!カッコつきで代入することさえ忘れていなければ、ばらして書く必要もないですね。細かく書くと次のようになります。
$$2x^2=2(x)^2=2 \times (-3)^2=2 \times 9=18$$
レベル3:\( \quad x^2 \times x^3 \quad(x=-2)の値\)
\(x^2 \times x^3\) が \(x^6\) になると勘違いしていませんか? 分からなくなったら書き下してみましょう。
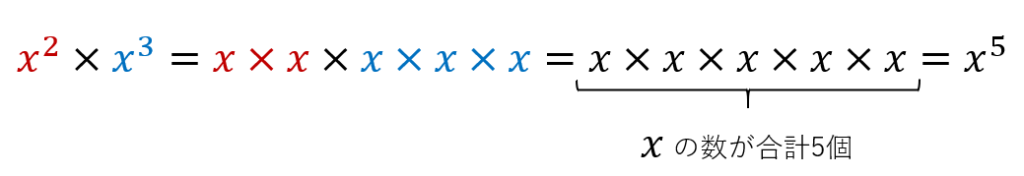
上の式から \(x^2 \times x^3\) は \(x^5\) ですね。右上にくる数(指数)は 2×3 ではなく、 2+3 です。掛け算ではなく足し算であることに注意しましょう。ここに \(x=-2\) を代入しましょう。上のレベル2でも説明したようにカッコつきで代入することを忘れずに。
$$ x^5=(-2)^5=-32 $$
これが答えです。累乗の計算のおススメは先に符号を決定してしまうことです。マイナスは2つ重なるとプラスに変わります。今回マイナスは合計で5個ですね。
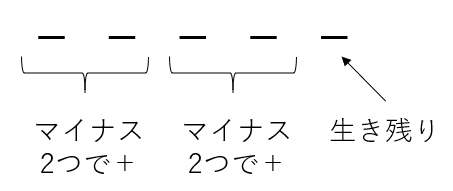
生き残りの -(マイナス)がいるので答えは - になることが確定します。すなわち - が偶数個で答えが + になり、- が奇数個で答えは - になります。今回の場合は - が5個(奇数個)存在しているため - になり、レベル2の問題では - が2個(偶数個)存在しているため答えは + になります。
レベル4:\( \quad x^2 y^3 \div (-x^3 y) \quad(x=-2,y=4)の値\)
複雑になっても焦らない!分からなくなったらばらすのだ!
$$\quad x^2 y^3 \div (-x^3 y)=\frac{x^2 y^3}{-x^3 y}=\frac{x \times x \times y \times y \times y}{-x \times x \times x \times y}$$
あとは同じ文字同士削除していきましょう。
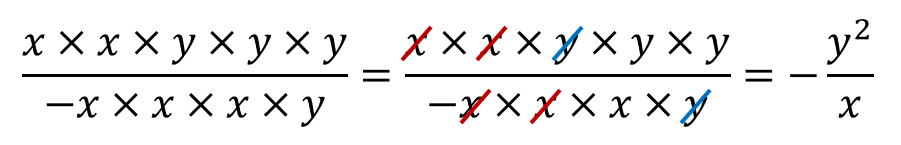
ここに値を代入しましょう。
$$ -\frac{y^2}{x}=-\frac{(4)^2}{(-2)}=-\frac{16}{(-2)}=8$$
これが答えです。
レベル5:\( \quad x^3 y^2 \div (-x^3 y)+x^2 y^2\times xy^2 \quad(x=-2,y= \frac{1}{2})の値\)
最後の問題。今までのレベル1からレベル4を駆使すれば解けます。まずはレベル3、レベル4で学んだ通りに計算を進めましょう。
$$\quad x^3 y^2 \div (-x^3 y)+x^2 y^2\times xy^2=-y+x^3y^4$$
ここに代入。カッコつきです。
$$-y+x^3y^4=-\left(\frac{1}{2}\right)+(-2)^3 \left(\frac{1}{2}\right)^4$$
ここで、\((-2)^3\left(\frac{1}{2}\right)^4\)はレベル3で解説している通り - が3つ(奇数個)重なっているため - です。
よって答えは
$$-\frac{1}{2}+(-2)^3 \left(\frac{1}{2}\right)^4=-\frac{1}{2}-\frac{1}{2}=-1$$
今回はこれでおしまいです。お疲れさまでした。質問や感想、この問題解いてほしい要望等あればコメント欄に書いていただけると嬉しいです。できる限り対応します。


コメント