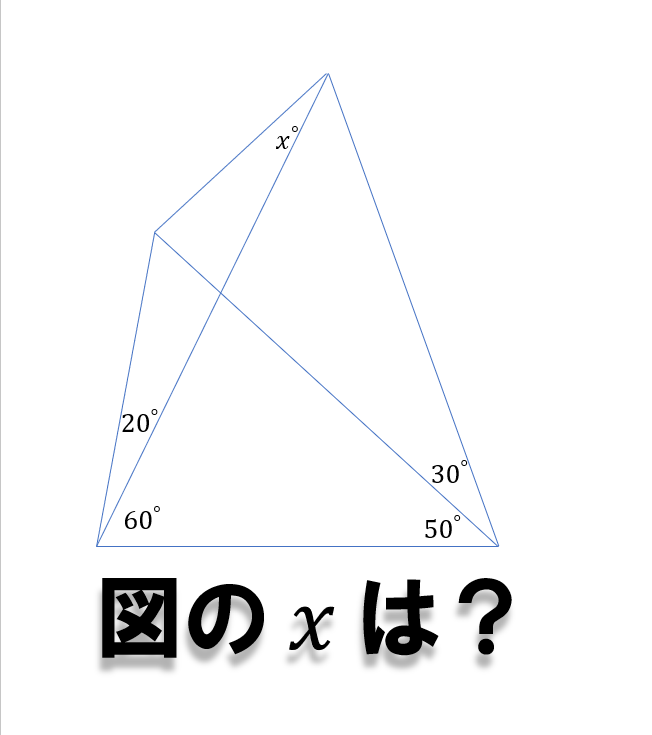
機械系に所属している私ですが,数学の方が好きです(笑).そんな私は小学生だったころ角度の問題にはまっていました.塾の先生から角度の問題をいただくとすぐに飛びついていました.そんな私,オー雅はワークの最後の問題で以下のような問題を見つけました.
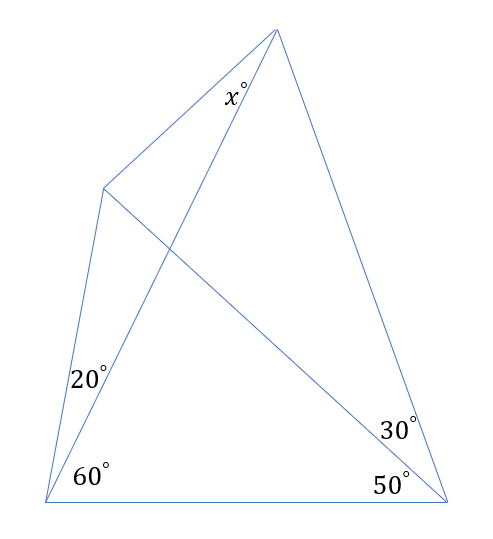
後々にこの問題はラングレーの問題と呼ばれている角度の難問だということを知りました.そんなことなど全く知らず立ち向かいました.結果授業中の隙間時間はほぼこの問題に尽くして1年間かけてやっと解きました(笑).有名な解法としては2つが主流らしく,その補助線をFigure2 に示します.少しでも立ち向かいたいと思った人はこれ以降は見ずにペンを動かしてみてください!!
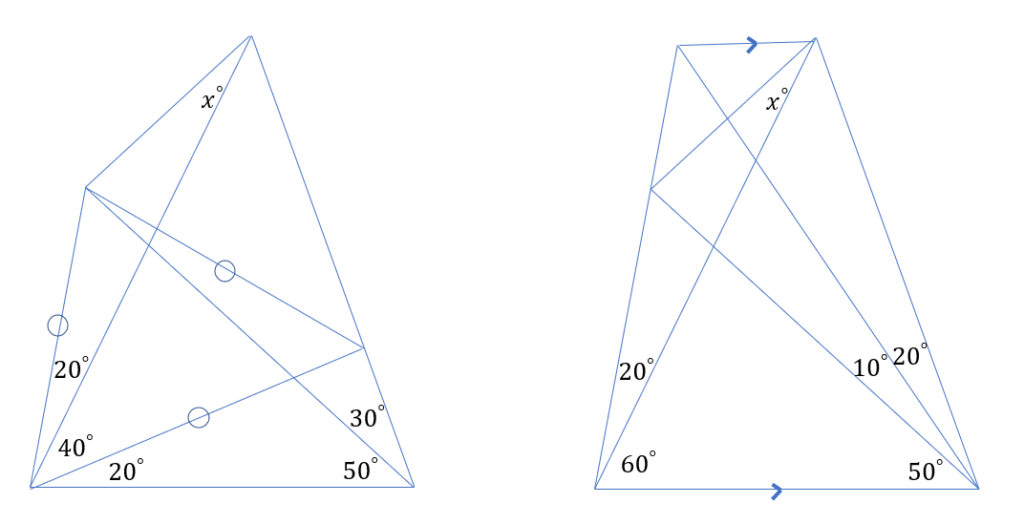
正直,補助線を与えられた状態でもかなりの難問…
私が思いついたのはFigure 2のパターン1でした.しかし,1年かかっている…. 私は補助線2本以上書かないといけない問題は難しすぎると思っています.ふつう浮かばない!浮かんだとしても今回みたいに膨大な時間がかかる.しかし解いたのは小学生のころだし…24歳になった今なら知識が増えたしすぐに求められるのでは?と思って再挑戦しました.高校生の三角関数を使った解法です.考えた補助線をFigure 4に示します.
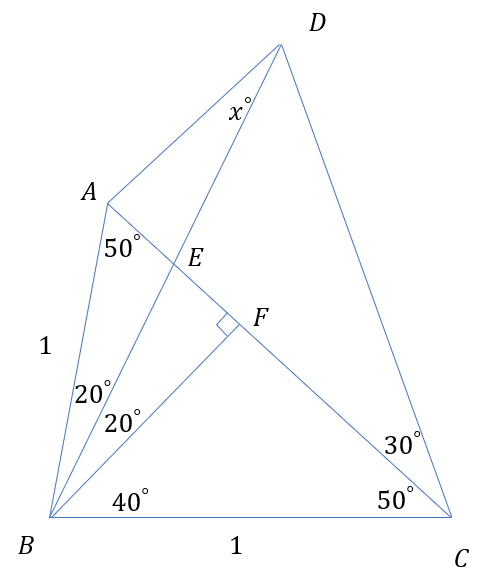
補助線はBFの1本しか引きません!△ABCはBA=BCの二等辺三角形なのでBA=BC=1として解きました.この時,正弦定理と三角関数の知識を用いて無理やりAEとEDを求めます.
$$AE=\frac{\mathrm {cos} 50^\circ}{1+ \mathrm {sin} 50^\circ }$$
$$ED=\frac{\mathrm {cos} 50^\circ}{1+ \mathrm {sin} 50^\circ }\times \frac{1+2\mathrm {sin} 50^\circ}{2\mathrm {cos} 50^\circ }=AE \times \frac{1+2\mathrm {sin} 50^\circ}{2\mathrm {cos} 50^\circ } $$
というわけで以下の三角形に落とし込める.
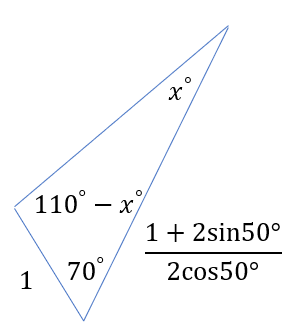
後は正弦定理で角度を求めていくのみ.
$$\frac{ \frac{1+2\mathrm {sin} 50^\circ}{2\mathrm {cos} 50^\circ }}{ \mathrm {sin} (110^\circ-x^\circ) }=\frac{1}{\mathrm {sin} x^\circ } $$
実はこの式を変形するのはとても大変でした.そして心臓に悪い.途中でsin20°等が絡むのですが,とても扱いづらい.10°置きの三角関数の値って3の倍数以外のもの(10°とか40°)とかって求められるけどとてもしんどい.というか扱えたものではない.カルダノの公式(3次方程式の解の公式)を用いる必要がある(はず).この解の公式の答えがやばい!気になる人は調べてみてください.何はともあれ,この式は上手いこと計算出来て x=30 と出てきます.夜の12時47分に開始して2時6分に終了.所要時間:1時間19分.昔に比べたらめちゃくちゃ早い(笑)!我ながら上出来です.

コメント