どうも,オー雅です.今回も正五角形について取り上げます.今回は対角線の長さを求めていきます.前回の角度編の延長のものとなりますので,見てない方は是非そちらからご覧いただいた後にこちらの記事を見ていただけると幸いです.では参ります.
問題
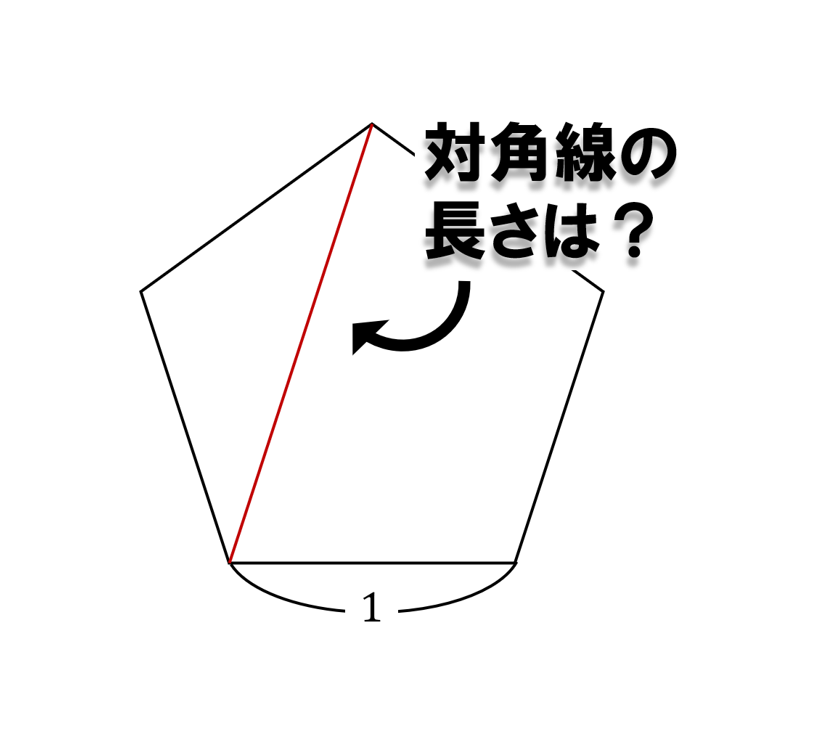
赤色の対角線の長さを求めてください.解説には前回の角度編の図を用います.そして補助線を2本使います.正直初見ではなかなか厳しいと思いますが,是非考えてみてください.
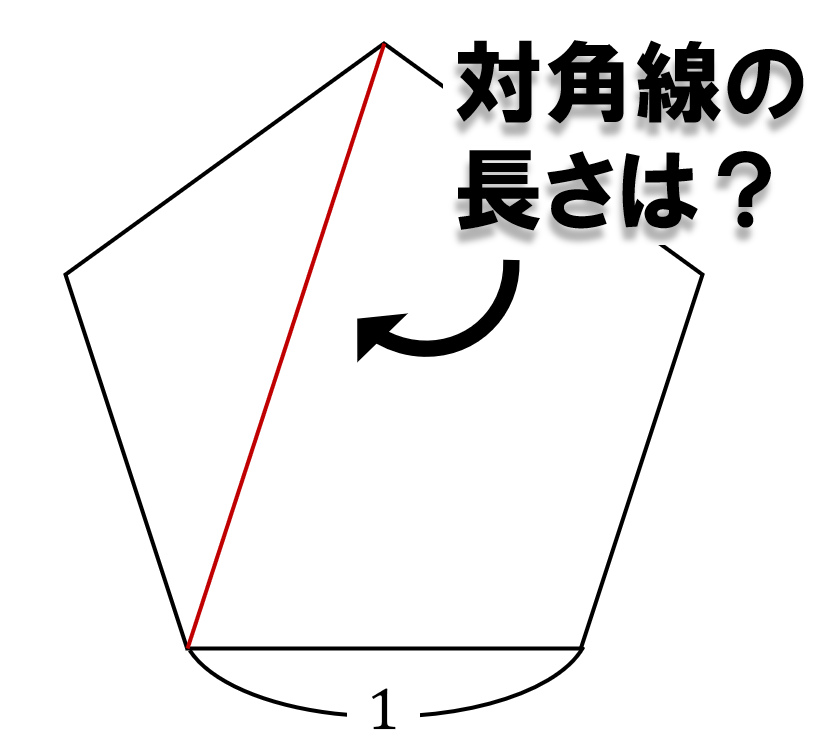
解き方
では補助線を引いていきます.
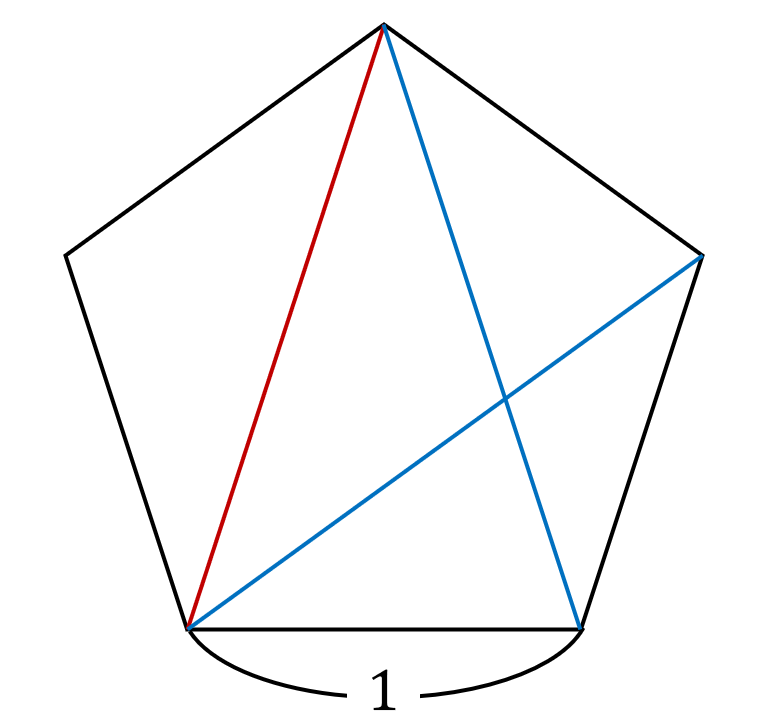
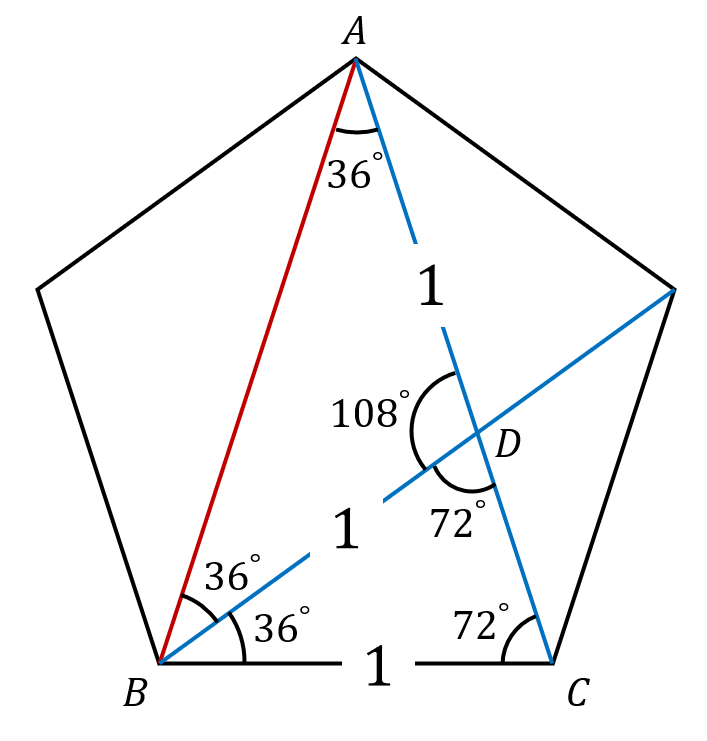
そして角度編に従って角度を書き込みます.
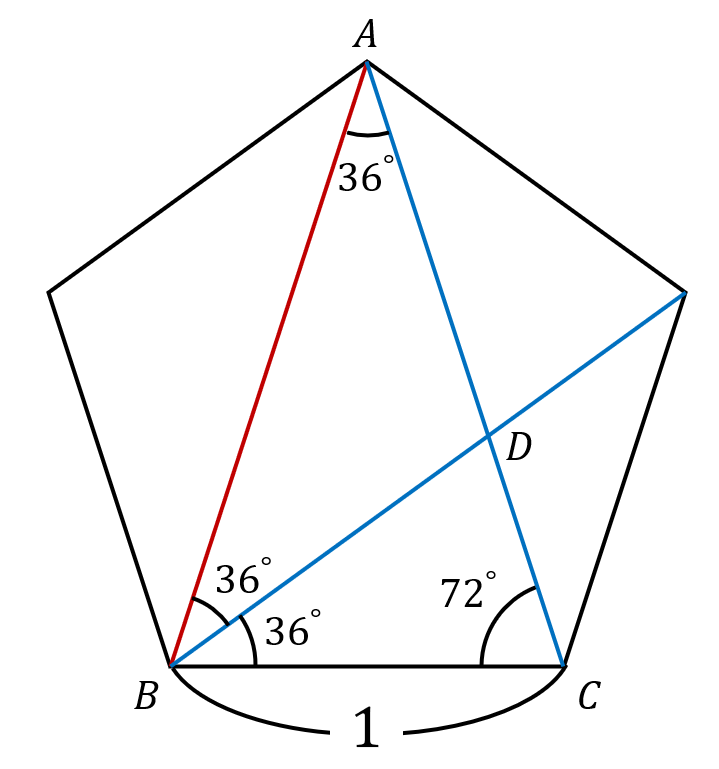
三角形の内角の和は\(180^\circ\)であることから他の必要な角度も書き込みます.
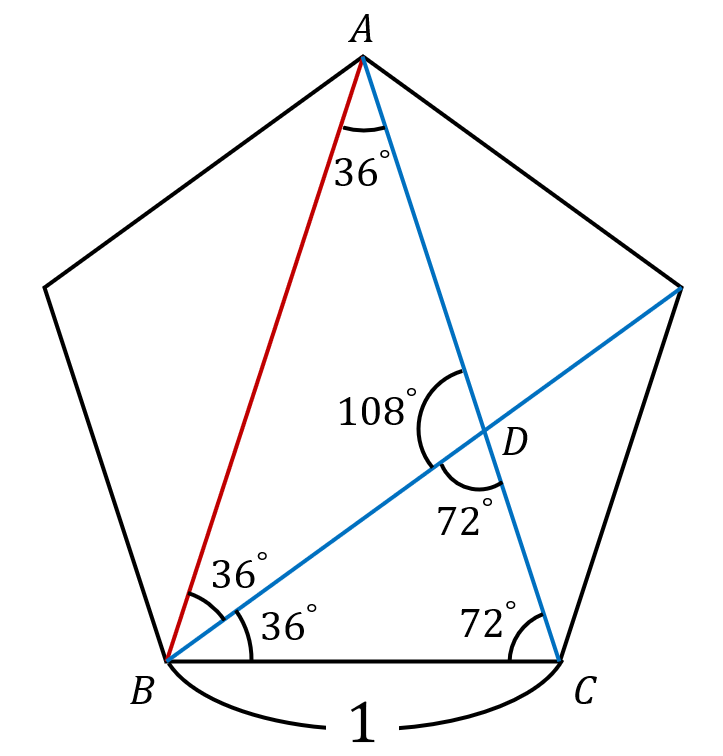
下準備完了!ここからはたくさんある二等辺三角形に注目して長さを書き込んでいきます.
△BCDは∠Bを頂角とする二等辺三角形なので,BC=BD.
△ABDは∠Dを頂角とする二等辺三角形なのでBD=AD.
以上より,BDとADはBCと同じ長さ1と分かります.
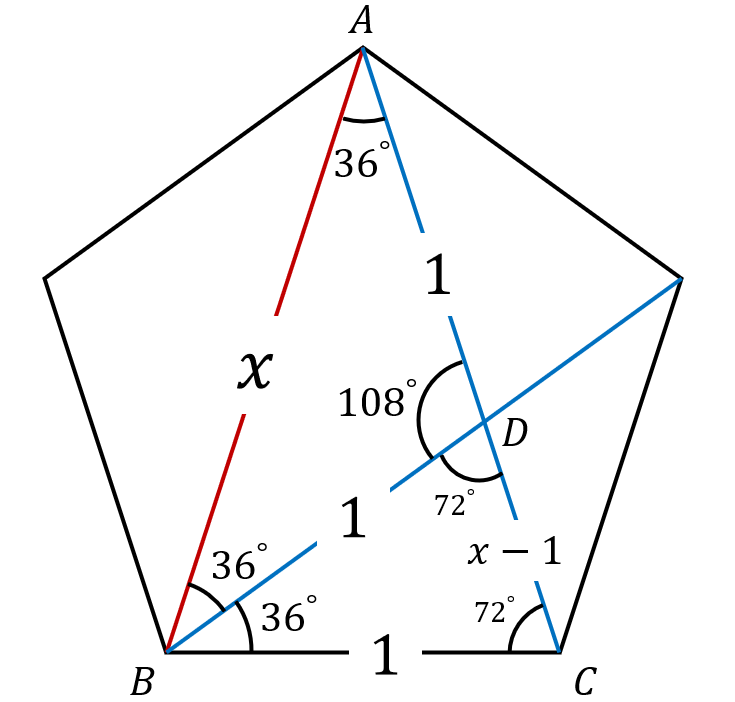
そして,今求めたい赤色の長さを\(x\)と置くと,△ABCは∠Aを頂角とする二等辺三角形なので,ACの長さも\(x\)になる.DCの長さはこの\(x\)から1を引くことで\(x-1\)と分かる.
あと少しです!頑張ってください!
△ABCと△BCDは2組の角度がそれぞれ等しいので相似.
よって,
$$ AB:BC=BC:CD $$
$$x:1=1:x-1$$
この式を解いて
$$x=\frac{1+\sqrt{5}}{2}$$
今回はここまで.次の正五角形について知ってる?-作図編-では正五角形の作図をしていきます.乞うご期待!

コメント