どうも、オー雅です。 今日は時計に関する問題。問題文はいたってシンプル。しかし、どこから手を付ければいいか悩みそうな問題です。私の経験上、問題文が短いほどヒントが少なく、解きにくい問題が多いように感じます。地道に式を立てて正解にたどり着くこともできますが、あることに気づけば暗算でも解けるといった面白い問題です。
問題
12時ぴったりの時計がある。次、時針と分針が重なるのは何時間後か?
ヒント
分からなかったら実際に動く時計を眺めてみるといいかもしれません。そして、大体いつぐらいに交わりそうか見当をつけておきましょう。答えを出しやすくなったり、ミスの軽減につながったりします。1時の段階ではまだ交わってないですね。1時5分から1時10分の間くらいになるのでは…?
解答
パターン①
分針は1時間で1周する。時針は12時間で1周する。よって、\(x\)時間たった時には分針は \(x\) 周、時針は \(\frac{x}{12}\) 周する。
そして12時を過ぎた後に時針と分針が交わるときは、分針が時針に対して1周の周回差をつけた時である。(以下の図で言えば、分針(青色)は1周以上しているが、時針(赤色)は1周もしていない。)
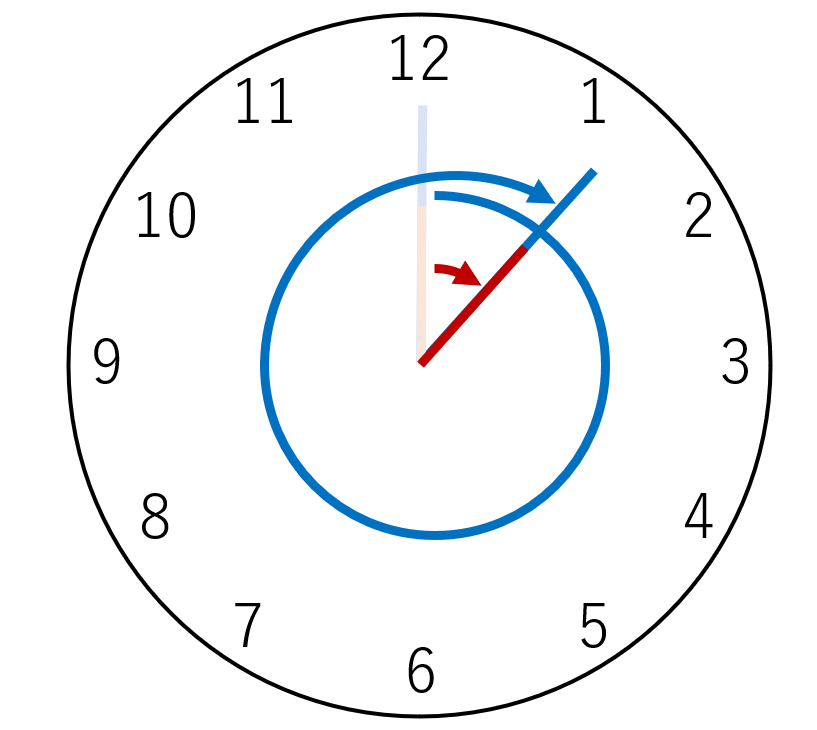
つまり、分針が\(x\)周してる間に時針は \(\frac{x}{12}\) 周して、その差が1周である。
よって \(x\)時間後に時針と分針が交わるとした時、以下の式が成り立つ。
$$x-\frac{x}{12}=1$$
これを解いて、\(x=\frac{12}{11}\)
よって、求める答えは \(x=\frac{12}{11}\) 時間後。
実際 \(x=\frac{12}{11}\)時間は大体1時間と5分くらいです。ヒントの章で見当をつけておくことをお勧めしました。見当と出した答えを比べて、答えが正しいかを吟味することで正答率アップにつなげていきましょう。
パターン②
時計が12時から次の12時になるにかけて、同じ間隔で10回長針と分針が交わる。
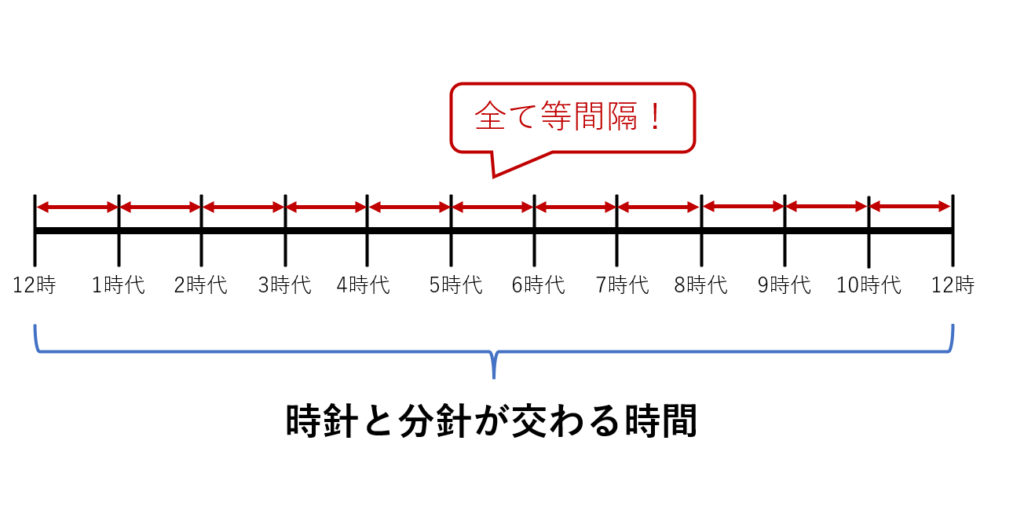
上の図に注目すると、等間隔で示した赤色の矢印は11個で12時間を占める。よって、赤色の矢印1個あたりは \(\frac{12}{11}\)時間。これが答え。
オー雅のコメント
パターン①は方程式を解いて地道に解いていく解法でした。計算は簡単ですが、問題の意味を理解して立式までするのに時間がかかりそうな問題です。同じような問題と言えば、兄弟が池の周りをぐるぐるする問題と一緒です。パターン②は気づけばそうかとなりますが、なかなか浮かばなそうな発想です。しかし浮かんだら暗算で解けてしまうのが面白いところですね!
今回はこれでおしまいです。お疲れさまでした。この問題に対する質問や感想、こちらの解き方はどうですか?などの提案、間違いの指摘等をコメント欄に書いていただけると嬉しいです。できる限り対応します。

コメント