どうも、オー雅です。数学はほかの科目とは違って覚えることが少ないです。とはいえ、覚えておかないものも存在します。その1つが今から紹介する円やおうぎ形、球の公式です。覚えないといけないとはいえ、覚えるコツがあるので紹介しようと思います。
円
円の公式は以下の2つ。
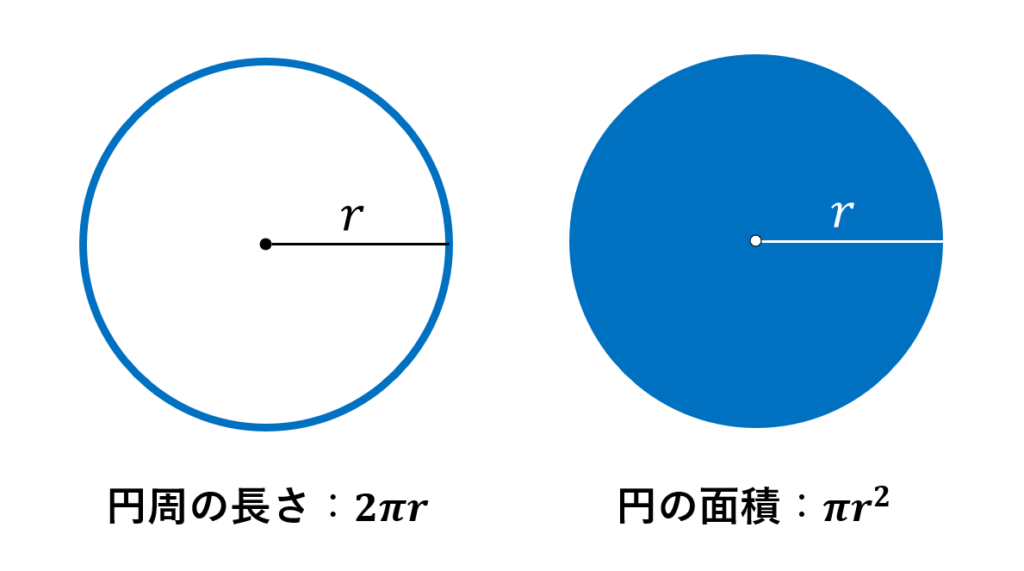
うろ覚えな人やどっちがどっちだか分からなくなってしまう人いますよね?
そんな時は単位に着目しましょう!
身近な面積の例を浮かべてみましょう。
$$(長方形の面積)=(縦の長さ)×(横の長さ)$$
$$(三角形の面積)=(底辺の長さ)×(高さ)×\frac{1}{2}$$
どちらも長さが2回かかっているのが分かると思います(高さも長さに含まれますよね)。これらを見て分かることは面積は長さを2回かけなければならないことです。
面積の単位って \(\mathrm{m^2}\) だったり \(\mathrm{cm^2}\) だったりしますがこの2っていうのは累乗の2を表しているんですよね。だから、
$$\mathrm{m^2=m \times m} $$
$$\mathrm{cm^2=cm \times cm} $$
こうやってみると面積は長さを2回かけなければならないって分かりますよね!
円で考えてみても同じです。
円の面積を表す \(\pi r^2\) を累乗を使わずに表してみると、
$$\pi \times r \times r$$
長さ(半径\(r\))が2回かけられていますね。
この単位に注目する考えは数学だけでなく理科にも使えます。この考えを持っておくと大分有利だと思うので是非参考にしてみてください。
もう1つの公式である円周の長さ:\(2 \pi r\)は
$$2\times \pi \times r$$
長さを求める公式なので、長さ(半径\(r\))は1個しか式の中に無いですね。
ここで注意です。
長さをかけると面積になりますが、長さを足しても長さのままです。
以下に例を示します。
$$\mathrm{4cm \times 5cm =20cm^2}$$
$$\mathrm{4cm+5cm=9cm}$$
そして、単位の違うものを足したり引いたりは普通しません。
体重kgと身長mを足したりすることはしないということですね。これらのことに注意していれば、ミスしていても途中で何かおかしい!と思えるようになります。
この調子で次はおうぎ形にいってみましょう。
おうぎ形
おうぎ形のコツはずばりピザを想像すること!ピザハットでもピザーラでもドミノピザでも構いません!
以下の図を見てください。

1枚食われていることは気にせず…。8枚にピザが分割されていますね。なので、1枚当たりの面積は全体の面積の8分の1です。
おうぎ形について考える時は、あらかじめ360枚にピザが分割されていると考えましょう。まぁ厳密に言えば\(360^\circ\)枚に分割されています。そして、何枚のピザを食べていいかは中心角という言葉で表されます。
つまり、ピザが届いて、分割されて、そのうち何枚か食べますよね?
この文章を数学の言葉で書き直すと、
円が届いて、\(360^\circ\)枚に分割されて、中心角だけ食べます。
つまり、おうぎの周の長さは以下の式で求められます。

同じく、おうぎの円の面積は、

図では以下のようになります。
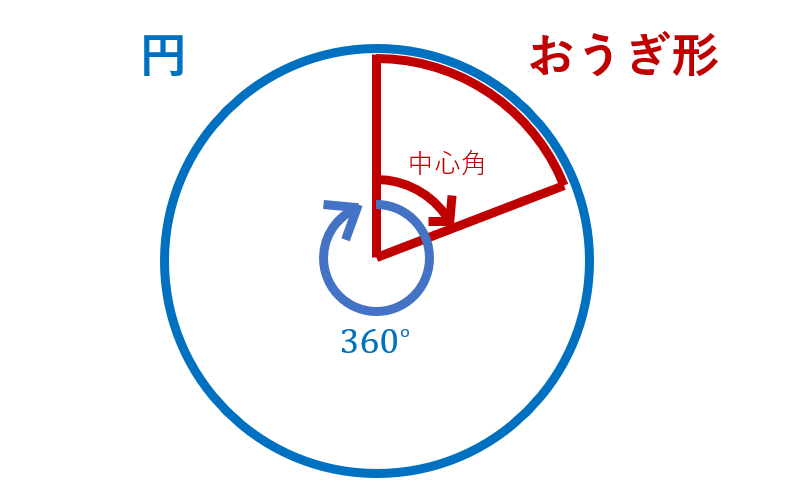
この調子で次は球にいってみましょう。
球
球の公式は以下の2つ。

ここでもどっちがどっちか分からなくなってしまう人は単位に注目しましょう。
立方体や直方体の体積を求める際には(縦)×(横)×(高さ)で求めます。つまり、体積を求めるには長さを3回かけなければなりません。
球の体積に注目してみましょう。ちゃんと長さ(半径\(r\)) が3回かけられているのが分かると思います。しかし分数だし覚えにくそうですね。私が中学生の時は以下のような語呂合わせを先生から教えていただき、その通りに覚えていました。数字との対応を確認しながら声に出して覚えましょう。対応する部分を同じ色にしてあります。

続いて球の表面積です。

面積なので、 長さ(半径\(r\)) が2回かけられていることを確認。そこに球の体積でも書いた「心配」がかかっていると覚えていれば十分だと思います。
今回はこれでおしまいです。お疲れさまでした。この問題に対する質問や感想、こちらの解き方はどうですか?などの提案、間違いの指摘等をコメント欄に書いていただけると嬉しいです。できる限り対応します。



コメント