どうも、オー雅です。毎年行われている数学オリンピック。毎年答えは一般公開されているのですが、その過程は公開されていません。2021年の問題は正答率を見てもわかる通り普段より難しくなっております。気になる人は公式サイトを調べてみてください。ここでは、私なりの10問目の解答を紹介しようと思います。
問題
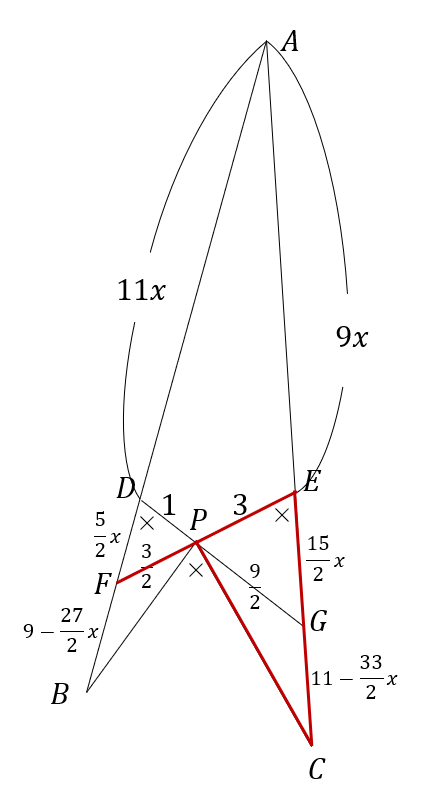
図において \( \frac{BP}{CP} \) の値を求めよ。(実際の問題は図が与えられていないのが恐ろしいです…。)
ただし、同じ印をつけた角度は等しい。\( DBCE \) は同一円周上に存在。\( AB=9, AC=11, DP=1, EP=3 \)
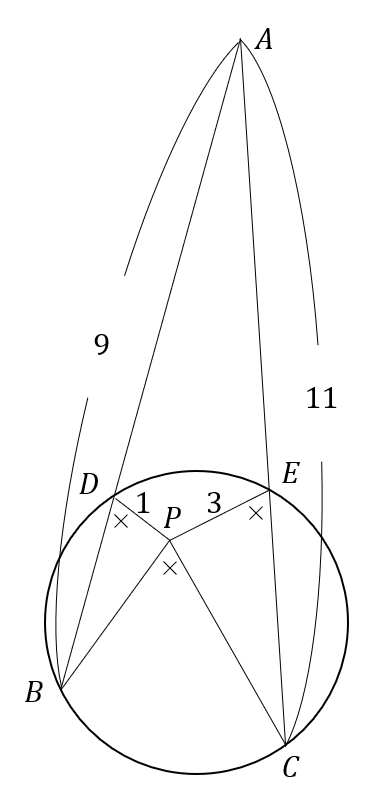
解答
方べきの定理より、\( AB:AC=AE:AD=9:11 \) であるから、\( AE=9x,AD=11x\) と置ける。
そして、\( PE \) と \( AB \) の交点を \( F \) 、\( PD \) と \( AC \) の交点を \( G \) と置く。
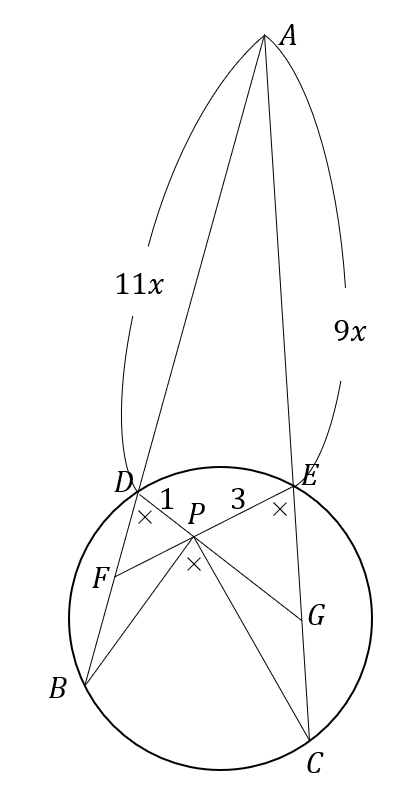
\( △PDF \) と \( △PEG \) は相似。よって、\( DP:EP=DF:EG=FP:GP=1:3 \) であるから、\( DF=y, EG=3y,FP=z, GP=3z\) と置ける。
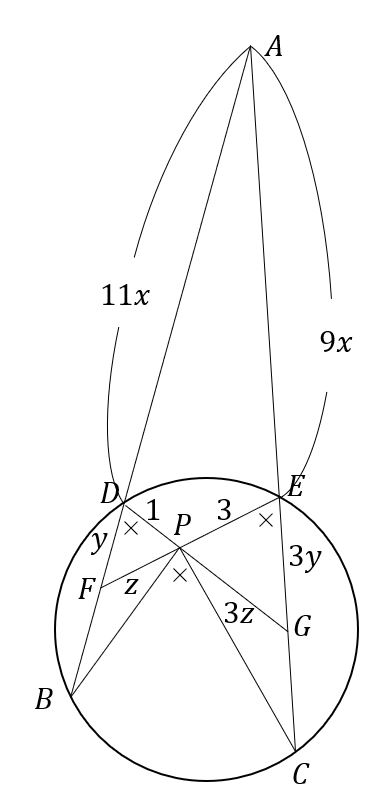
\(△AEF\) と \(△ADG\) は相似。よって、\(AE:AD=EF:DG=9:11 \)。
$$ (3+z):(1+3z)=9:11 $$
$$ ∴ \quad z= \frac{3}{2} $$
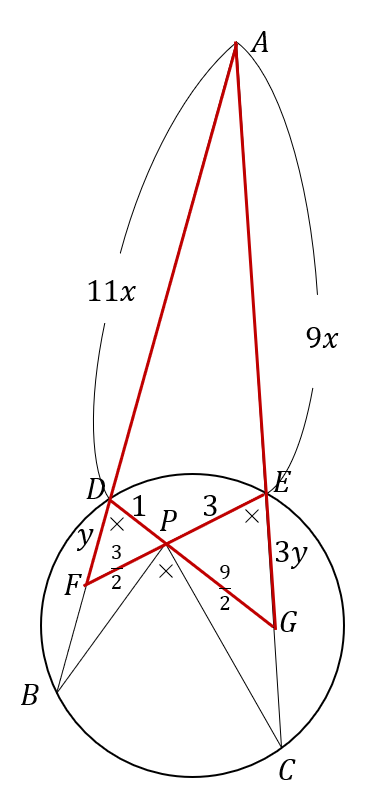
図の赤色部分においてメネラウスの定理より、
$$ \frac{DF}{AD} \times \frac{PE}{FP} \times \frac{GA}{EG}=1 $$
$$ \frac{y}{11x} \times \frac{3}{\frac{3}{2}} \times \frac{9x+3y}{3y}=1 $$
$$ ∴ \quad y= \frac{5}{2}x $$
よって、
$$ FB=AB-AD-DF=9-11x-\frac{5}{2}x=9-\frac{27}{2}x $$
$$ GC=AB-AE-EG=11-9x-\frac{15}{2}x=11-\frac{33}{2}x $$
図の赤線部に注目し、\( ∠PCG+∠GEP=∠CPB+∠BPF \) かつ \( ∠GEP=∠BPF \) であるから、 \( ∠PCG=∠BPF \)。同様に、\(∠CPG=∠PBF\)。
よって、\(△PCG \) と \(△BPF \) は相似。
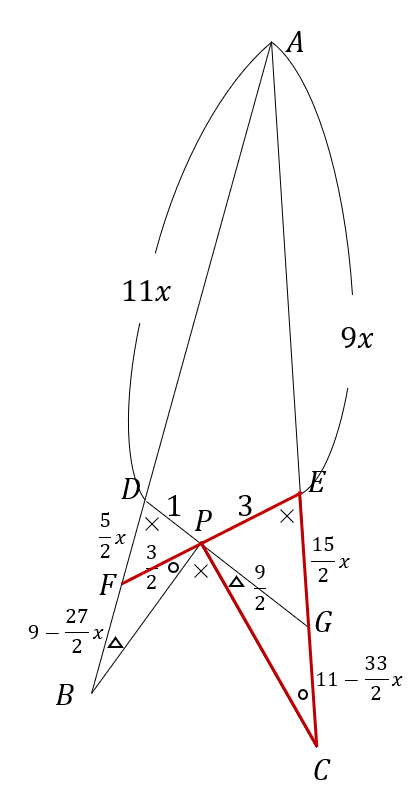
よって、
$$ GC:GP=FP:FB $$
$$ (11-\frac{33}{2}x):\frac{9}{2}=\frac{3}{2}:(9-\frac{27}{2}x) $$
$$ ∴ \quad 1-\frac{3}{2}x= \sqrt{\frac{3}{11 \times 4 }} $$
よって、\(△PCG \) と \(△BPF \) が相似であることも加味し、
$$ \frac{BP}{CP}=\frac{FB}{GP}=\frac{9-\frac{27}{2}x}{\frac{9}{2}}=2 \times (1-\frac{3}{2}x)=\sqrt{\frac{3}{11}}=\frac{\sqrt{33}}{11} $$
これが答え。
オー雅のコメント
とにかく時間がかかりました。問題読み間違えてるのに気づくのに20時間。答えにたどり着けるまでに20時間。いろいろな方法を試してこの解法にたどり着きました。一番時間かかったのは同じ角度を見つける部分です。言われてみれば単純ですが、浮かびませんでした…。
今回はこれでおしまいです。お疲れさまでした。この問題に対する質問や感想、こちらの解き方はどうですか?などの提案、間違いの指摘等をコメント欄に書いていただけると嬉しいです。できる限り対応します。



コメント