さぁいよいよ数学オリンピック予選最終問題です。実際の数学オリンピックは解答のみを提出して、過程は提出しません。そのため、当てずっぽうでも答えが分かれば点数がもらえます。今回のこの問題、当てずっぽうで当てた人はいると思います。しかし、これが答えと確信を持てた人は本番ではいなかったのではないかと思うくらい難しいです。では参ります。
問題
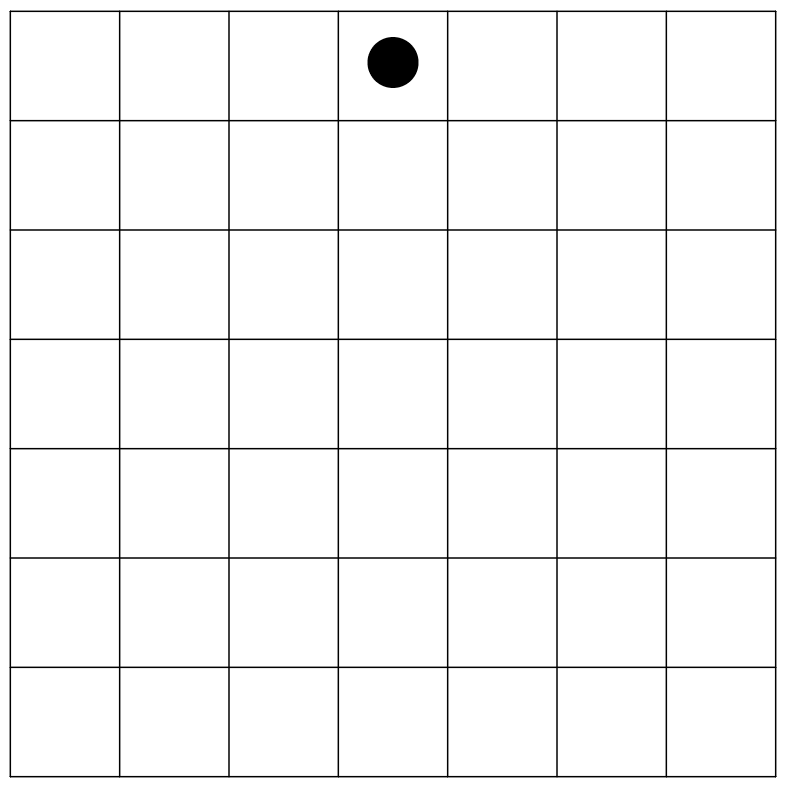
図のように7×7マスの盤面に1つの駒が置かれている。駒は以下のような4通りの行動ができる。
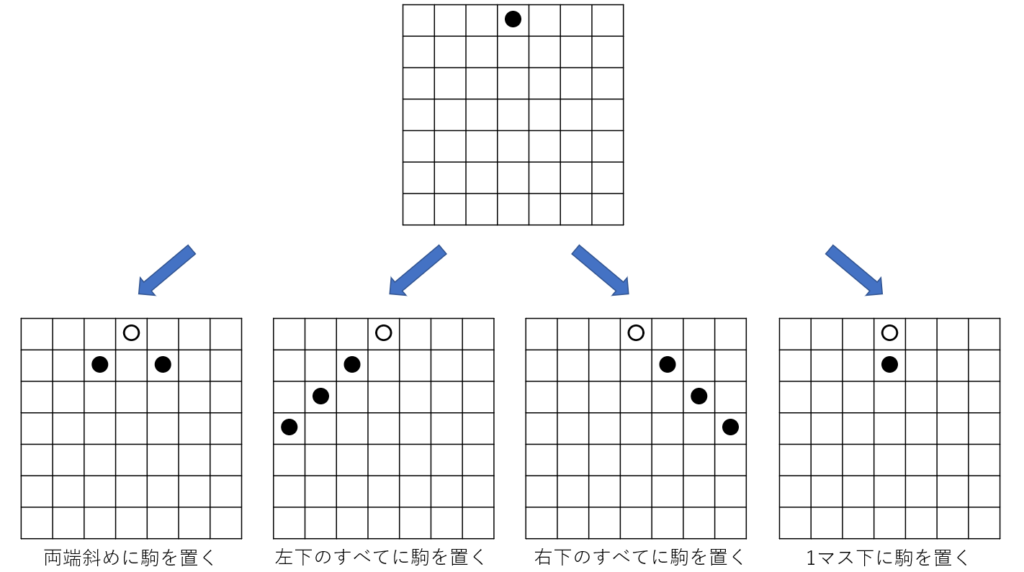
ただし、いずれの行動をしても行動した駒は消える。すでに駒が存在している場合は駒は置かない。この行動を任意の回数繰り返した時、駒は最大何個まで増やせるか?
詳しくはこちらを参照ください。
オー雅の思考回路
まずは実際にやるしかないな。最大何個になるか予想はついてもそれが最大になる理由を説明するのは厳しそう…。本番なら当てずっぽうで答えるしかない…。
解答
するべきことは以下の2つです。
ⅰ) 19個の通りを見つける。
ⅱ)20個以上が存在するとした時、矛盾を見つける。
ⅰ)は実際に行ってみてください。複数通りあります。鬼門はⅱ)です。ⅱ)の説明を今から行っていきます。
以下のように盤面に数字を振る。
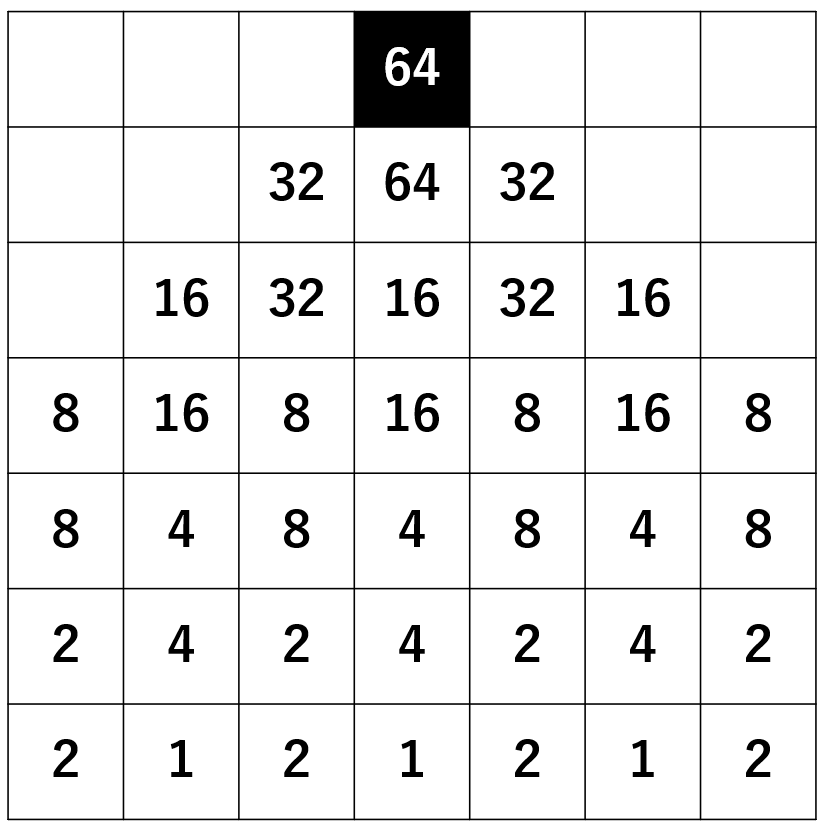
この時、駒が置かれている場所に書かれている数字の総和は、駒の行動によって変わらないもしくは減少する。よって、数字の総和は盤面がもとにいた場所に書かれていた64を超えることはできない。数字の総和が64を超えないように盤面を埋めていったとき、駒を置ける最大の個数は19個である。(例えば以下のように埋めた時、駒の個数は19個で数字の総和は59。)
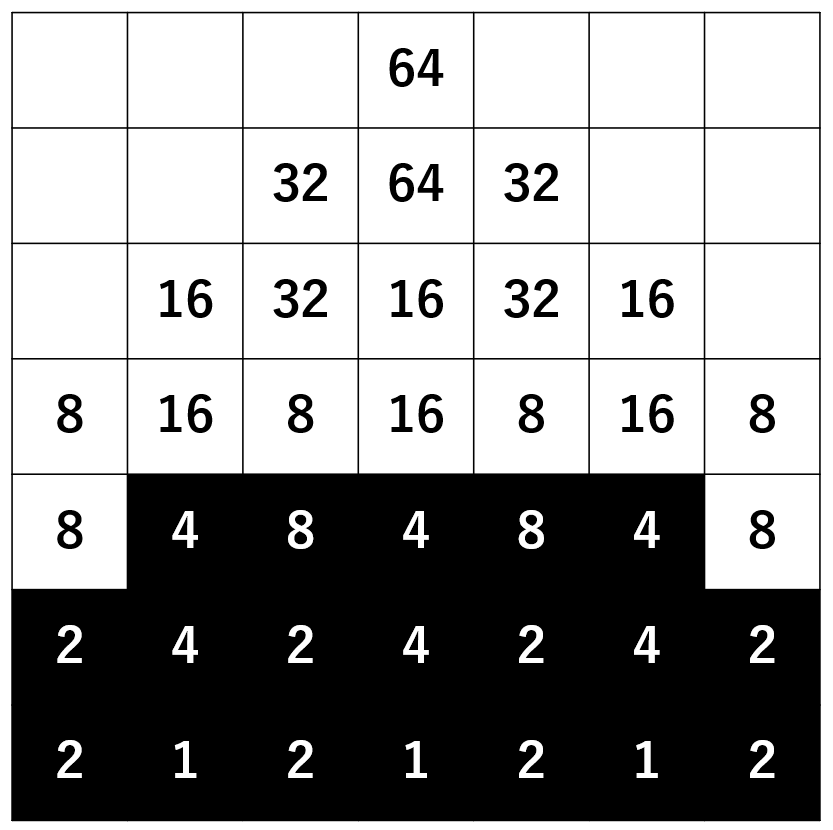
よって、20個以上が存在しないことが示された。
ⅰ),ⅱ)より、求める駒の最大の個数は19個。
オー雅のコメント
この解法を本番で思い浮かべられるのは余程の天才しかいないのではないでしょうか?この解法の第1の関門は最大が19個であるという仮定を立てられること。そして第2の関門は20個以上が存在すると矛盾が生じることを述べること。どちらかが抜けてしまっては解答として成立しなくなってしまいます。とにかくⅱ)はやばい!
今回はこれでおしまいです。お疲れさまでした。この問題に対する質問や感想、こちらの解き方はどうですか?などの提案、間違いの指摘等をコメント欄に書いていただけると嬉しいです。できる限り対応します。



コメント