数学オリンピック2021年予選第1,2問

どうも、オー雅です。毎年行われている数学オリンピック。毎年答えは一般公開されているのですが、その過程は公開されていません。2021年の問題は正答率を見てもわかる通り普段より難しくなっております。気になる人は公式サイトを調べてみてください。ここでは、私なりの1,2問目の解答を紹介しようと思います。

第1問

2つの素数 $ m,n $ が $ m+n=90 $ を満たしているとき、 $ mn $ の最大値を求めよ。

$ m+n=90 $ より、$ m=90-n $

よって、 $ mn $ は以下のように表せる。

$$mn=(90-n)n $$

この式を式変形（平方完成）し、

$$(90-n)n=-(n-45)^2+2025 $$

よって、グラフは以下のようになる。

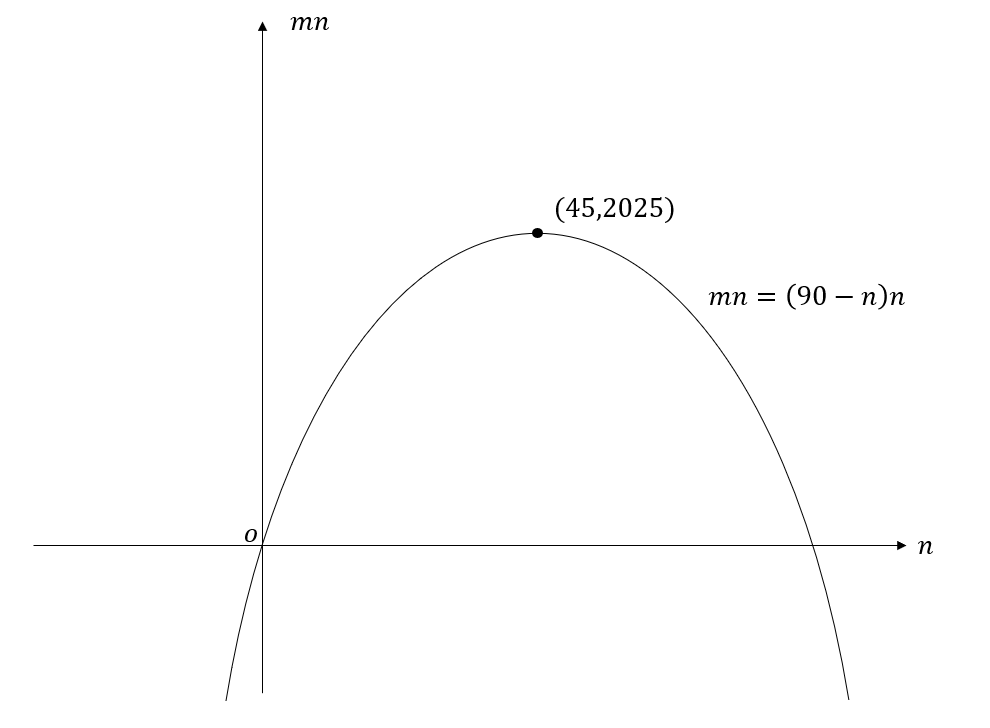
グラフより、 $n$ が $45$ から離れるほど値が小さくなる。$45$ に最も近い素数は $43,47$ の2つ。それぞれ、$n=43$ のとき、$m=47$ で $mn=2021$。$n=47$ のとき、$m=43$ で $mn=2021$。よって、求める答えは $2021$。

$m \geq n$ の縛りを入れて、$45 \geq n$ としておけばもっとシンプルに解答が書けます。

$m \geq n$ とし、$m=45+a, n=45-a \ ( a\ は \ 0 \ 以上の整数)$ とする。この時、 $mn$ は以下のように表せる。

$$mn=(45+a)(45-a)=2025-a^2$$

$a$ が小さいほど値が大きい。$a$ が $0,1$ の時は $m,n$ が素数にならない。$a$ が $2$ の時、$m=47, n=43$ でともに素数であり、$mn=2021$。これが答え。　

パターン1はよくある解法だと思います。その中でも青線のような工夫を出来ると時間短縮につながります。パターン2は発想力や経験値が必要です。その分、解答はシンプルで時間も大幅に短縮できるのがメリットです。

下図の面積が $1$ の正十角形において、青色部の面積の和を求めよ。

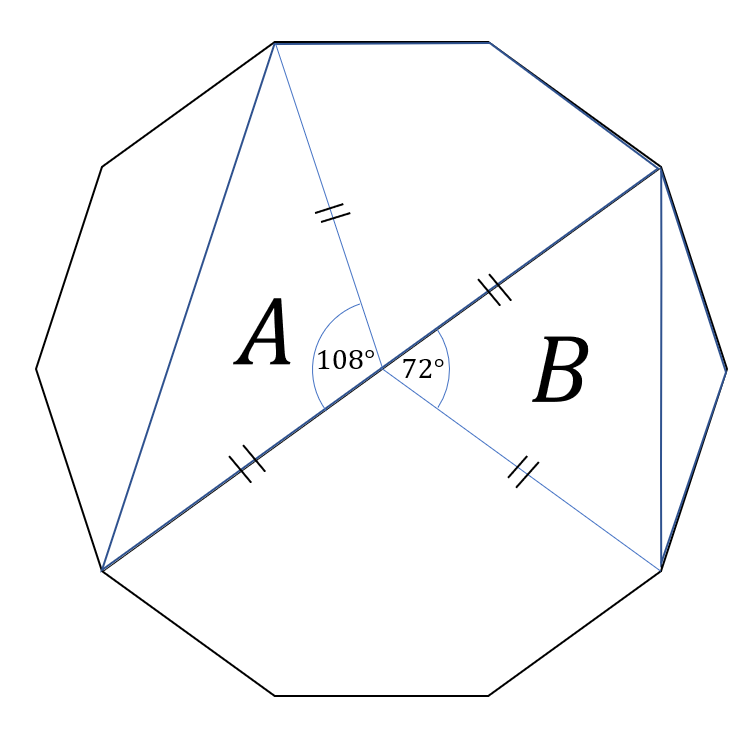
図に表したエリア $A,B$ について考える。

図に印をつけた辺の長さは全て等しい。この辺の長さを $r$ と置く。

$$ (エリアAの面積) = \frac{1}{2} \times r \times r \times \mathrm{sin}108 ^\circ $$

$$ \qquad \qquad \qquad\qquad\qquad \ = \frac{1}{2} \times r \times r \times \mathrm{sin}(180^\circ-108 ^\circ)$$

$$ \qquad \qquad \qquad\qquad \qquad\qquad \quad \ = \frac{1}{2} \times r \times r \times \mathrm{sin}72^\circ=(エリアBの面積)$$

よって、エリア $A$ とエリア $B$ の面積は等しい。

だから、以下の青色の面積を代わりに求めればよい。

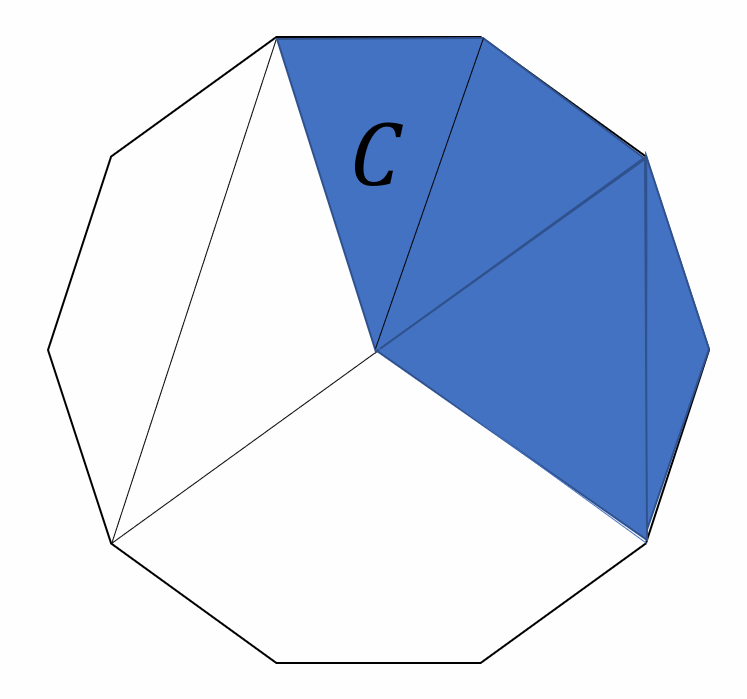
この正十角形はエリア $C$ が10枚敷き詰められている。そして、合計の面積は $1$であるため、エリア $C$ の面積は $ \frac{1}{10} $

よって、エリア $C$ 求める面積は

$$ \frac{1}{10} \times 4=\frac{2}{5} $$

これが答え。

別解多数です。是非、他の解法でも解いてみてください。実はこの解法にたどり着くまでに20分以上かかってしまいました…。

今回はこれでおしまいです。お疲れさまでした。この問題に対する質問や感想、こちらの解き方はどうですか？などの提案、間違いの指摘等をコメント欄に書いていただけると嬉しいです。できる限り対応します。