どうも、オー雅です。毎年行われている数学オリンピック。毎年答えは一般公開されているのですが、その過程は公開されていません。2021年の問題は正答率を見てもわかる通り普段より難しくなっております。気になる人は公式サイトを調べてみてください。ここでは、私なりの9問目の解答を紹介しようと思います。1問目から8問目もいずれ書いてみるつもりです。
問題
2021×2021のマス目の各マスに1,2,3の数を1つずつ書き込む方法であって,どの2×2のマス目についても,その4マスに書かれている数の総和が8になるようなものが全部でA通りあるとする。このとき,Aを100で割った余りを求めよ.ただし、回転や裏返しにより一致する書き込み方も異なるものとして考える.
オー雅の思考回路
まずは左上の2×2マスをすべて書き出してみて、それぞれについて何通りあるか考えようかな。
解答
2×2マスを総和が8になるように1,2,3の数で埋める通りは以下の通り。
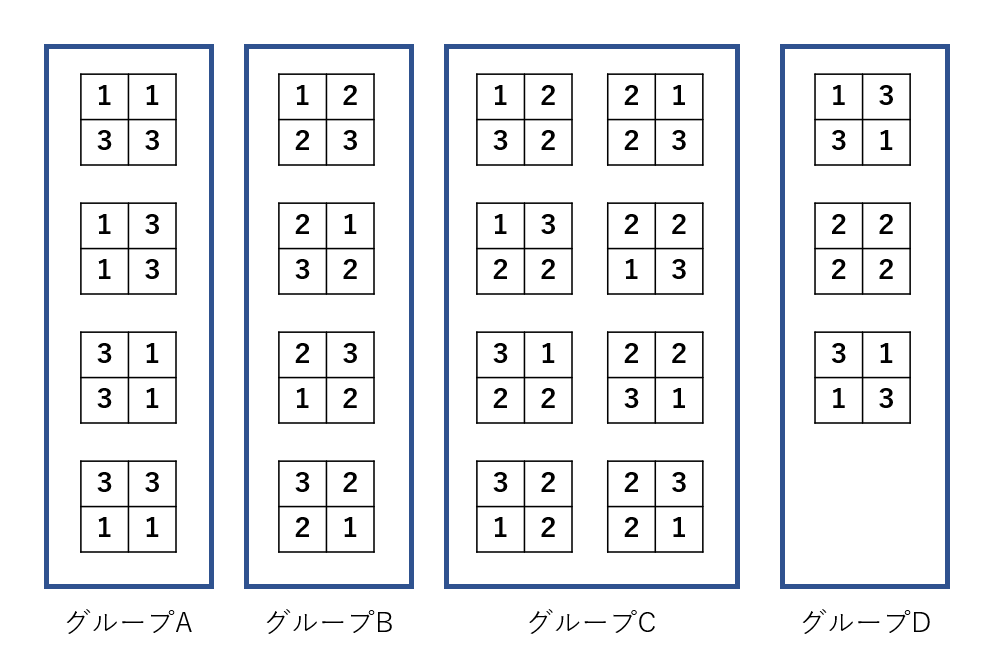
ⅰ)グループAについて
グループAの一番上のものについて考える。
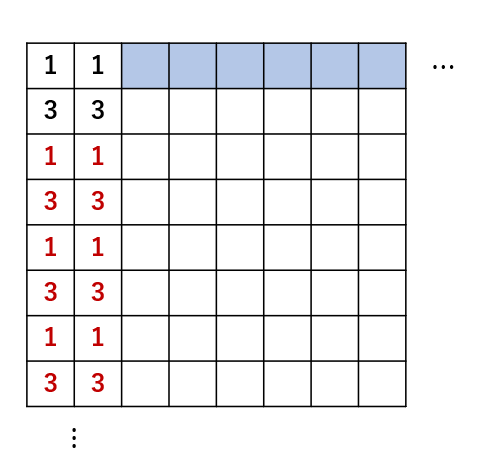
赤色で示した部分は確定。(4つのマスについて3が2つ入っている段階で合計が6なので次の2マスは1が2つ入るしかありません。もし2や3を埋めようとすると残りの1マスが0以下になってしまいます。次に1が2つ入っている段階で3が2つしか入るしかありません。これを繰り返していく。)次に、青色の部分を埋めていく。青色が埋まり次第残りの空白のマスは全て埋まっていく。ここで青色のマスは何を入れても(1,2,3どれでも)空白のマスは1,2,3のいずれかで埋めることが出来る。このことは実際に証明してみるか書いてみて確かめてみてください。おそらく本番では証明している時間はないと思います。
他のグループAのものも同じ通り存在。
ⅱ)グループBについて
グループBの一番上のものについて考える。
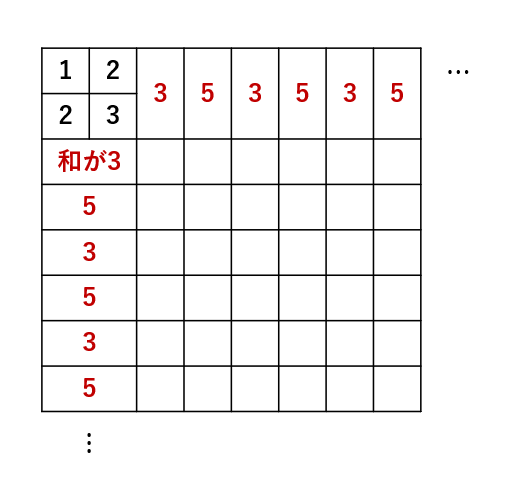
和が3のペアの埋め方は(1,2),(2,1)の2通り。和が5のペアは(2,3),(3,2)の2通り。このペアで図の赤を埋めていくと、残りの空白マスが定まる。ここでも、空白マスは必ず1,2,3のどれかのいずれか(証明略)。
他のグループBのものも同じ通り存在。
ⅲ)グループCについて
グループCの左上のものについて考える。
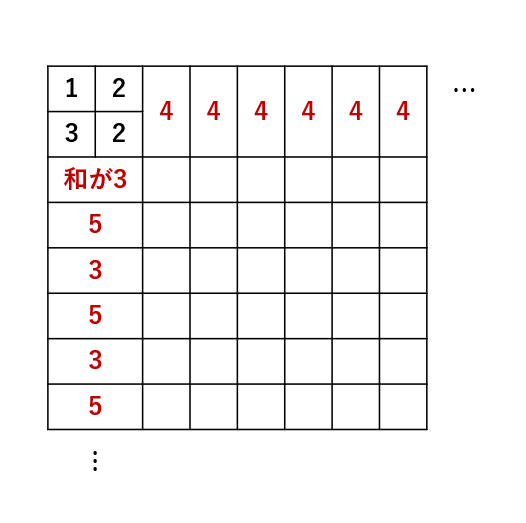
和が3のペアの埋め方は(1,2),(2,1)の2通り。和が5のペアは(2,3),(3,2)の2通り。和が4のペアは(1,3),(2,2),(3,1)の3通り。よって和が3の左マスには1or2,和が5の左マスには2or3,和が4の上マスには1or2or3の可能性が存在。ここで、和が3,5の左マスに2を使用しなかった場合、和が4の上マスに1,2,3どれを埋めても残りのマスを1,2,3のいずれかで埋めることが可能。しかし、和が3,5の左マスに1度でも2を使用した場合、奇数列目の上マスは1or2で埋めること、偶数列目の上マスに2or3で埋めた時のみ残りのマスを1,2,3のいずれかで埋めることが可能(証明略)。
他のグループCのものも同じ通り存在。
ⅳ)グループDについて(オー雅はこの処理法が浮かぶのに時間がかかりました。)
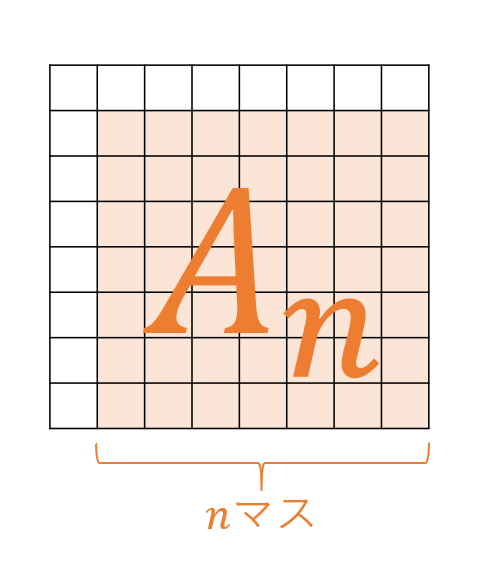
n×nマスを1,2,3の数を1つずつ書き込む方法であって,どの2×2のマス目についても,その4マスに書かれている数の総和が8になるようなものが全部で\(A_n\)通りあるとする。この時、\(A_{n+1}\)通りの中で左上の4マスがグループDとなるようなものを\(A_n\)を使って表現することを考える。
a)\(A_n\)の内、左上が1のもの
グループDの内、右下が1のものはグループDの一番上のものだけである。
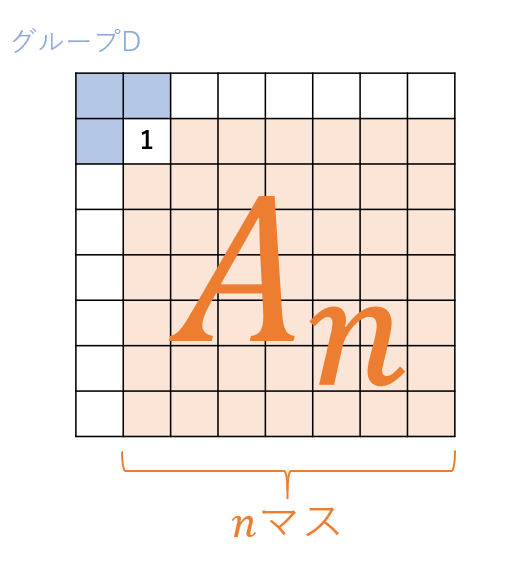
この時、残りの空白は自身と隣合わせのオレンジとの和が4になるように埋めればよい。
b)\(A_n\)の内、左上が2のもの
グループDの内、右下が2のものはグループDの真ん中のものだけである。
この時も、残りの空白は自身と隣合わせのオレンジとの和が4になるように埋めればよい。
c)\(A_n\)の内、左上が3のもの
グループDの内、右下が3のものはグループDの一番下のものだけである。
この時も、残りの空白は自身と隣合わせのオレンジとの和が4になるように埋めればよい。
a,b,cより、\(A_{n+1}\)通りの中で左上の4マスがグループDとなるようなものは\(A_n\)と表現することが可能。
ⅰ,ⅱ,ⅲ,ⅳより、
$$A_{n+1}=4 \times 3^{n-1} +4 \times 4^{n-1}+8 \times(4^{n-1}+3^{n-1}-2^{n-1})+A_n$$
$$A_2=19$$
右辺第1項はⅰに、右辺第2項はⅱに、右辺第3項はⅲに、右辺第4項はⅳに対応。
これを解いて、
$$A_{2021}=2 \times(3^{2021}-3)+(2^{4042}-4)-2 \times(2^{2021}-2)+3$$
ここで、2の累乗、3の累乗を100で割った余りを考える。
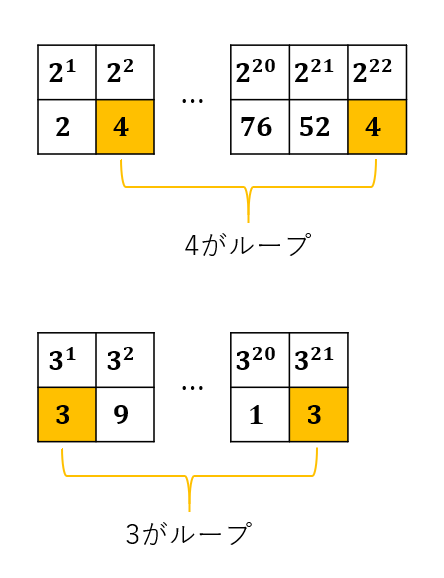
よって、
\begin{eqnarray} A_{2021} & \equiv & 2 \times(3-3)+(4-4)-2 \times(52-2)+3\\ & \equiv & 3 \qquad \mathrm {(mod100)} \end{eqnarray}
以上より、求める答えは3
今回はこれでおしまいです。お疲れさまでした。この問題に対する質問や感想、こちらの解き方はどうですか?などの提案、間違いの指摘等をコメント欄に書いていただけると嬉しいです。できる限り対応します。



コメント