どうも、オー雅です。今日はちょっと悩む図形問題の紹介。図形問題は苦手とする人が多いです。だからこそ解けるようになれば周りと差がつけられます。そのためには1つ1つ着実に問題を解いて、解くコツを吸収していく必要があります。もし解けなくても解答を見て、「なるほど、勉強になったな」と感じられればガッツポーズしましょう!
問題
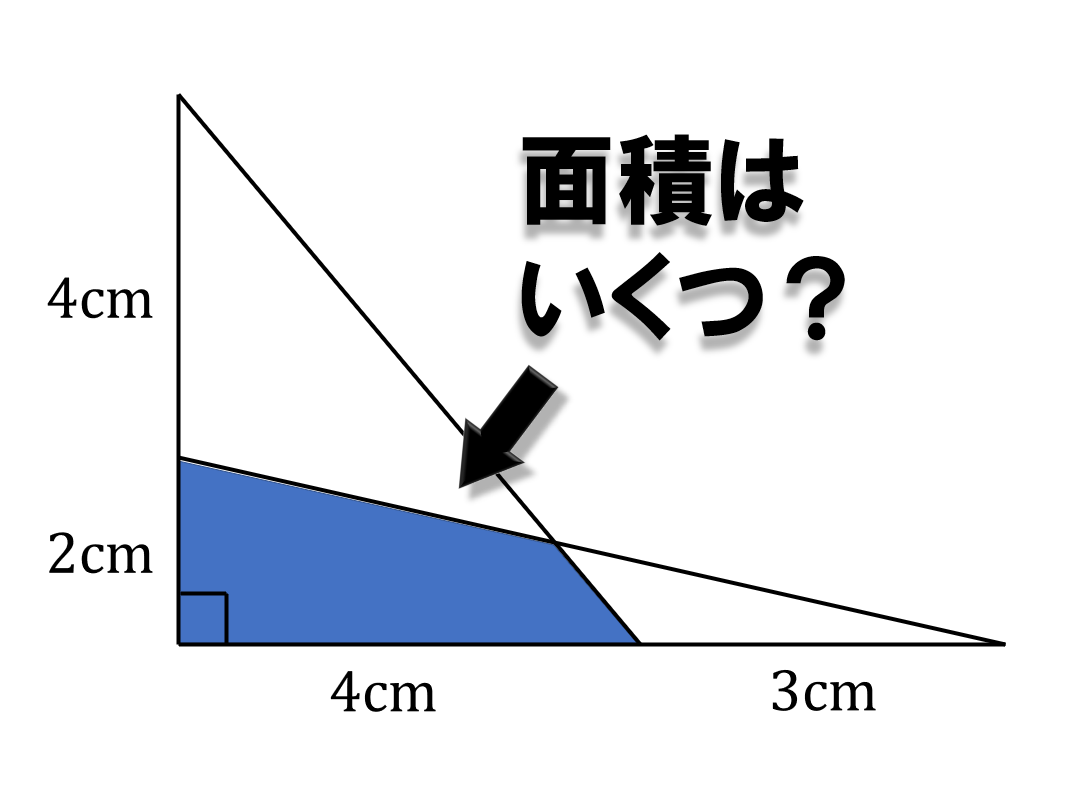
以下の青色の部分の面積を求めなさい。
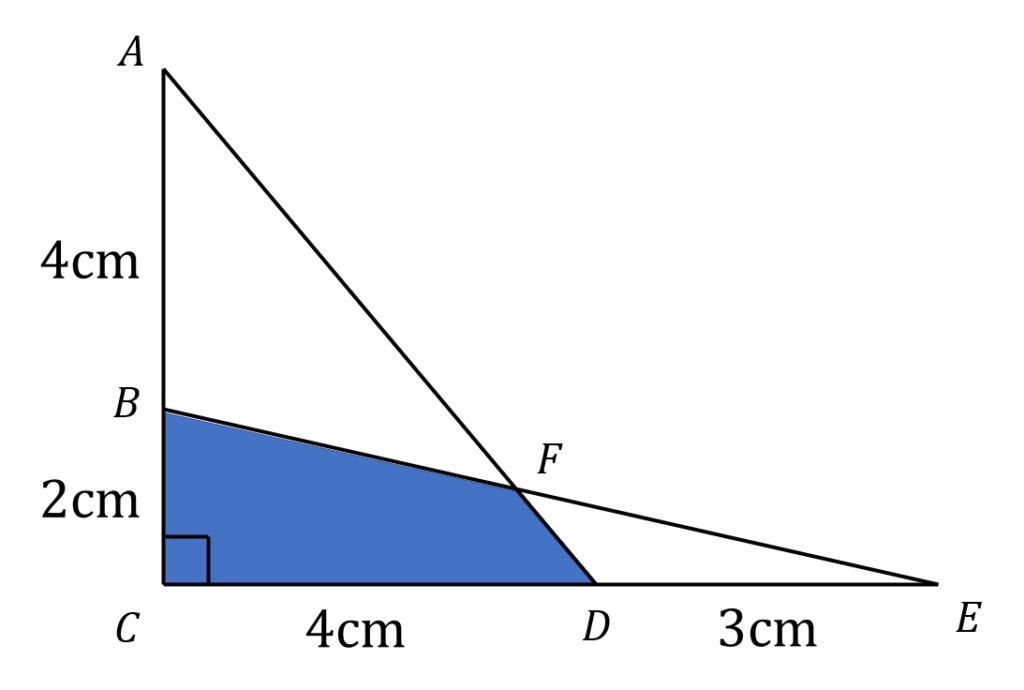
解答
パターン①
グラフを利用します。以下のように与えられた図形を座標に落とします。
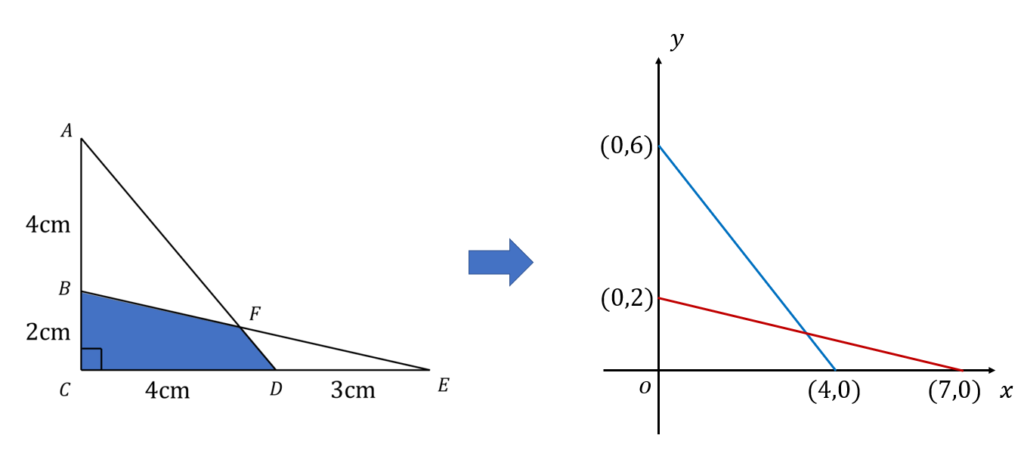
青色の直線は\((4,0),(0,6)\)の2点を通るから、直線の式は、
$$y=-\frac{3}{2}x+6\cdots①$$
赤色の直線は\((7,0),(0,2)\)の2点を通るから、直線の式は、
$$y=-\frac{2}{7}x+2\cdots②$$
①と②の連立方程式を解いて、青線と赤線の交点は、\((\frac{56}{17},\frac{18}{17})\)
よって、整理すると図のようになる。
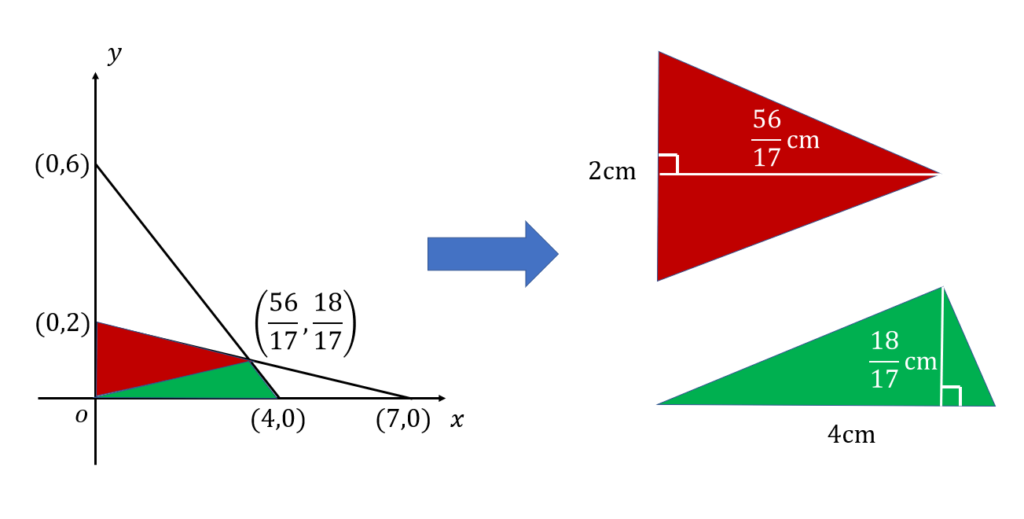
求めたい面積は、赤色の面積と緑色の面積の和なので、
$$2\times\frac{56}{17}\times\frac{1}{2}+ 4\times\frac{18}{17}\times\frac{1}{2}=\frac{92}{17} $$
これが答え。
パターン②
比を利用します。
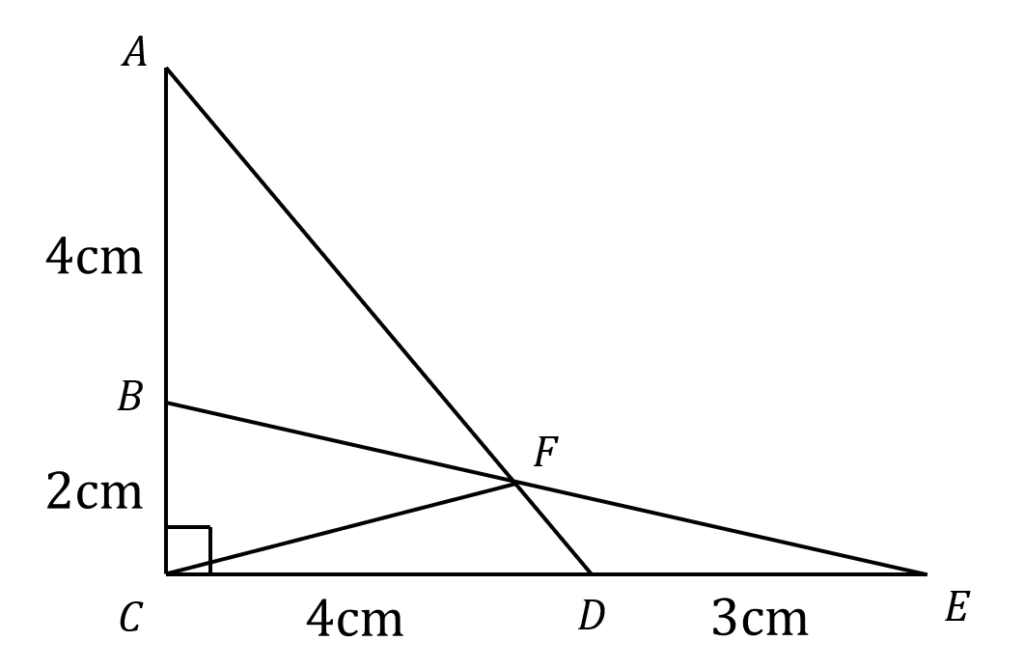
上の図において、\(△ABF\)と \(△CBF\) の面積比は\(4:2=2:1\)
また、 \(△CDF\)と \(△EDF\) の面積比は\(4:3\)
よって、以下のように文字を置ける。
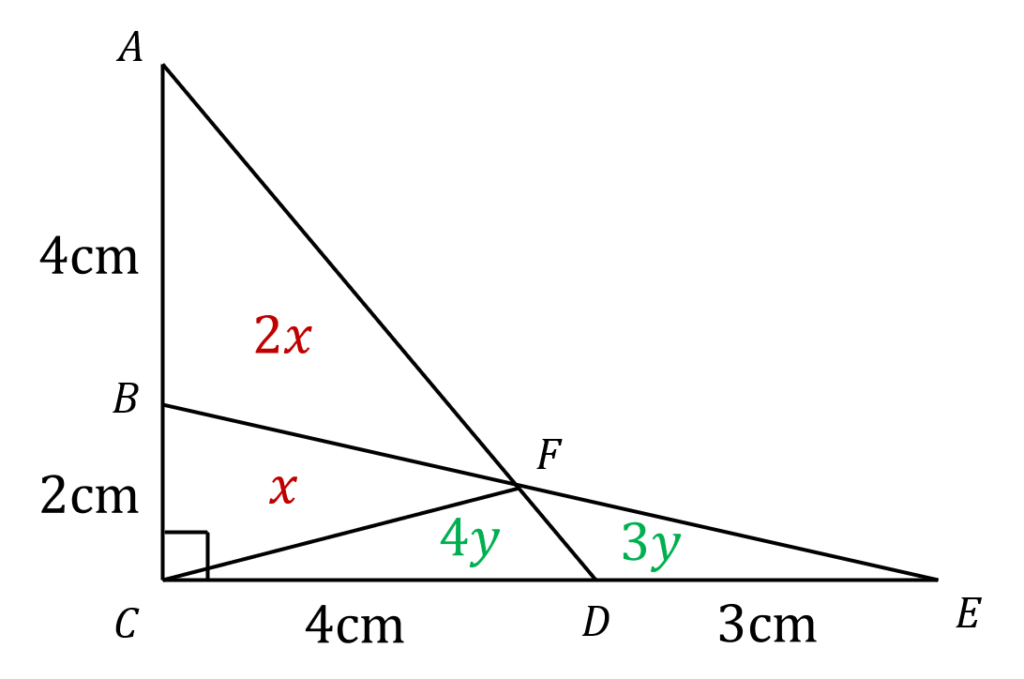
\(△ACD\)に注目し、
$$2x+x+4y=4\times(2+4)\times\frac{1}{2}$$
$$⇔3x+4y=12\cdots③$$
\(△ECB\)に注目し、
$$3y+4y+x=2\times(4+3)\times\frac{1}{2}$$
$$⇔x+7y=7 \cdots④ $$
③,④より、
$$x=\frac{56}{17},y=\frac{9}{17}$$
求めたい四角形の面積は\(x+4y\)で表せるので、
$$x+4y= \frac{56}{17} + 4\times\frac{9}{17} =\frac{92}{17}$$
これが答え。
オー雅のコメント
言われたらそうかとなるような問題でしたが、なかなか発想が難しかったと思います。キー坊とソー助にも相談し、メネラウスの定理を用いる、ベクトルを用いるなどの案が浮かびましたが高校数学になってしまうので割愛しました。気になった人は調べてみてください。
今回はこれでおしまいです。お疲れさまでした。この問題に対する質問や感想、こちらの解き方はどうですか?などの提案、間違いの指摘等をコメント欄に書いていただけると嬉しいです。できる限り対応します。


コメント